Формализация подхода разработки Web-интерфейсов к базам данных

Белорусский национальный технический университет

Кафедра инженерной математики

Методические указания к курсовым работам по информатике

для студентов второго курса

инженерных специальностей

приборостроительного факультета

Минск 2004

УДК

Данное издание предназначено для студентов второго курса приборостроительного факультета дневной и заочной формы обучения

Составители:

Нифагин В.А., Дубровина О.В.

Введение

Современной тенденцией в инженерных исследованиях и проектировании так же, как и в инженерном образовании является все более широкое использование компьютерного моделирования с целью максимального учета принципиально важных эффектов и оперирования полными математическими и информационными моделями объектов. Инженер-исследователь не должен находиться под прессом опасений, что получившаяся модель слишком сложна в формальном, вычислительном плане и что в связи с этим придется существенно «упрощать» задачу. Причем, возможно, до такой степени, что модель совсем перестанет быть похожей на реальный объект.

В рабочей программе по информатике содержание курсовой работы по предмету определяется как создание математической или информационной модели какого-либо явления или технологического процесса. Для заданной математической или информационной модели должны быть разработаны структуры данных, подобраны алгоритмы, написаны и отлажены программы и проведен анализ полученных результатов. Визуализация полученной информации предполагается в табличной и графической формах. При создании математической модели необходимо осуществить выполнение следующих разделов:

1. Анализ исходной информации и нахождение адекватных феноменологических соотношений описания.

2. Выбор математического аппарата и программного обеспечения для получения качественных и количественных результатов.

3. Построение укрупненной блок-схемы алгоритма программы.

4. Написание и отладка программы.

5. Сравнение полученных результатов и при необходимости уточнение и корректировка или обобщение модели.

Целью курсовой работы является закрепление теоретического материала и выработка навыков решения и расчета физико-математических, технических и инженерно-экономических задач, а также приобретение исследовательских навыков, связанных с решением поставленной задачи.

Общие требования к курсовой работе

1. Строгое соответствие содержания работы заданию.

2. Четкость и логическая последовательность изложения материала.

3. Убедительность аргументации.

4. Краткость и точность формулировок.

5. Конкретность изложения результатов работы.

6. Обоснованность выводов и рекомендаций.

7. Аккуратность оформления.

Исходным документом является задание на курсовую работу, в котором должны быть указаны: тема работы, исходные данные, состав работы с указанием объема ее отдельных частей, сроки выполнения этапов работы и ее окончания.

Задание на курсовую работу разрабатывается руководителем работы при возможном участии исполнителя и утверждается заведующим кафедрой. При выдаче темы коллективу студентов задание выдается отдельно каждому исполнителю, и в нем указывается объем и состав работы, предусмотренной для индивидуального исполнения.

Изменения в утвержденное задание могут быть внесены только с санкции заведующего кафедрой.

Состав и объем работы, а также отдельных ее частей, устанавливаются руководителем работы, в соответствии с числом часов, предусмотренных учебным планом.

Сроки выдачи задания на курсовую работу, выполнения отдельных этапов и всей работы в целом устанавливаются кафедрой в соответствии с учебным планом и утвержденным графиком работы студентов.

Структура работы

Курсовая работа должна содержать в указанной последовательности титульный лист, задание на курсовую работу, реферат, содержание (оглавление), перечень условных обозначений, символов и специальных терминов, список использованных источников, приложения.

Основная часть курсовой работы должна включать

1. Введение.

2. Теоретическая часть.

3. Постановка задачи и получение исходных данных.

4. Алгоритм решения.

5. Полученные результаты.

6. Анализ результатов

7. Заключение (выводы, предложения).

8. Приложение (Разработанные программы)

9. Список использованной литературы.

Заключение должно содержать оценку результатов курсовой работы, выводы и предложения.

В приложении помещаются материалы, не вошедшие в основную часть, необходимые для отражения хода работы или значимости полученных результатов, первичные документы исследований, распечатки кода программ и т.д.

Требования к оформлению работ

Курсовая работа должна быть оформлена в текстовом редакторе Word. Параметры страницы: поля левое 30 мм, правое 15 мм, верхнее и нижнее – по 20 мм, формат бумаги А4, книжная. Основной шрифт текста Times New Roman, 13 пт, межстрочный интервал одинарный, выравнивание текста по ширине страницы, абзацный отступ 1 см. Шрифт заголовков – 14 пт, полужирный выравнивание по центру страницы. Нумерация страниц внизу страницы по центру.

Иллюстрации, чертежи, схемы, диаграммы размещают после первого упоминания их в тексте.

Титульный лист работы оформляется в соответствии с Приложением 1.

Задание на курсовую работу должно быть подписано руководителем и исполнителем работы с указанием даты его выдачи и утверждено заведующим кафедрой. Рекомендуемая форма бланка задания приведена в Приложении 2.

В тексте работы при изложении обязательных требований должны применяться слова: «должен», «следует», «необходимо», «требуется, чтобы», «разрешается только», «не допускается», «запрещается», «не следует». При изложении других положений следует применять слова: «могут быть», «как правило», «при необходимости», «может быть»; «в случае» и т.д. При этом допускается использовать повествовательную форму изложения текста статьи, например «применяют», «указывают» и т.п.

В работе должны применяться научно-технические термины, обозначения и определения, установленные соответствующими стандартами, а при их отсутствии общепринятые в научно-технической литературе. В случае использования специфической терминологии по тексту должны быть приведены соответствующие разъяснения.

Следует выделить три основные направления в заданиях для курсовых работ.

1. Рассмотрение математических моделей с последующим численным анализом в рамках того или иного специализированного пакета.

2. Создание информационных моделей на базе соответствующих приложений. (БД, Internet, компьютерное проектирование).

3. Исследовательская работа, включающая создание замкнутого программного приложения.

Объединяющим признаком является форма ядра проектов. Как правило, это дифференциальные уравнения, обыкновенные и в частных производных или модели прикладной статистики. Хотя типовые проекты, являются учебными, они содержат исследовательскую интригу, имеют важные практические приложения и не являются тривиальными задачами в вычислительном аспекте. В проектах реализуется сочетание инженерной актуальности, с одной стороны, и относительно высокой математической (вычислительной) сложности, с другой, чтобы обеспечить достаточную мотивацию для обращения к какому-либо из современных математических программных пакетов.

Примеры курсовых работ по этим направлениям:

1. «Численное моделирование температурного поля платы компьютера». На примере теплопроводности рассматриваются численные методы для уравнений в частных производных второго порядка. Стандартные средства MathCad’ дополняются программой, позволяющей моделировать стационарные двухмерные температурные поля для существенно расширенного круга задач и корректно описывать разнообразные условия теплового взаимодействия объекта с окружающей средой. Распределение температурных полей показано на рис.1

.

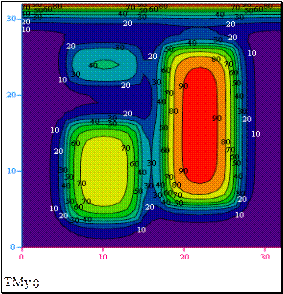
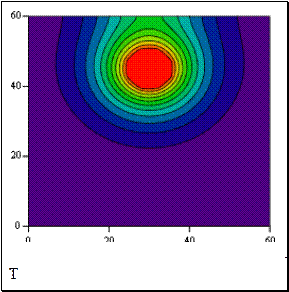
Рис. 1

Формализация подхода разработки Web-интерфейсов к базам данных.

Одной из типовых информационных моделей является создание разнообразных интерфейсов к базам данных в Internet. Поэтому актуальной является задача формализации создания произвольных Web-интерфейсов. В работе рассматривается наиболее полный набор логических компонентов, составляющих Web-интерфейс, с функциональной точки зрения и определяется последовательность шагов, ведущих к скорейшему и оптимальному способу разработки Web-интерфейса к базе данных.

Целью работы является формализация подхода к созданию наиболее типичного и полнофункционального Web-интерфейса к базам данных.

Речь идет о стандартном Web-интерфейсе. Прежде всего, это, как правило, система идентификации пользователей, призванная не допустить несанкционированный доступ к данным. Понятно, что само приложение должно содержать некую главную часть, предоставляющую пользователям доступ к данным с целью их просмотра и содержащую ссылки на остальной функционал системы. Под остальным функционалом подразумеваются система добавления и редактирования записей в базе данных, система удаления данных, система сортировки данных и поисковая система. Далее подробно рассматривается функциональный элемент, приводится экземпляр кода, реализующего наиболее типичную его форму, и последовательность выполняемых действий. При этом описан порядок его разработки, компоновки и взаимодействия отдельных его частей.

3. Создание приложения для файлового администрирования.

Программа для автоматизации рутинных операций по копированию/переносу/архивации файлов. Входящие файлы автоматически раскладываются по архиву с указанием текущей даты и времени, номера обрабатываемого файла. Предусмотрена возможность обработки сопроводительных документов к файлам, а также вывода списка входящих файлов, которые не могут быть обработаны при текущей конфигурации программы (не попадает ни под одну из масок файлов). Выполняется в виде консольного приложения, управляемого из текстовых конфигурационных файлов.

Темы курсовых работ в соответствии со специальностями

Специальность 38.01.01 Механические и электромеханические приборы и аппараты

1. Численное решение интегрального уравнения Фредгольма в контактной задаче о сдвиге покрытия на винклеровском основании в среде MathCad, MathLab.

2. Численное решение интегрального уравнения в задаче о колебании штампа в среде MathCad, MathLab.

3. Численное решение интегрального уравнения в контактной задаче о давлении штампа на другую полосу в пакетах MathCad, MathLab.

4. Распределение температуры в трубе квадратного сечения (задача Дирихле для уравнения Лапласа) в пакетах MathCad, MathLab.

5. Исследование характера изменения скорости тела в зависимости от времени движения при движении вверх (MathCad, Delphi).

6. Анализ поступательного движения тел MathCad.

7. Анализ вращательного движения тел MathCad.

8. Математическое моделирование колебаний маятника MathCad

9. Расчет траектории полета космического объекта вблизи Луны. MathCad.

10. Решение задачи о нахождении зависимости силы тока от времени методом Рунге-Кутта с помощью пакета MathСad.

11. Решение задачи о движении материальной точки с помощью пакета MathСad.

12. Решение задачи о тепловом режиме электрического тока с помощью пакета MathСad.

13. Определение передаточных функций динамических звеньев первого порядка на базе преобразования Лапласа с помощью пакета MathСad.

14. Определение передаточных функций динамических звеньев второго порядка на базе преобразования Лапласа с помощью пакета MathСad.

15. Определение передаточных функций динамических колебательных звеньев на базе преобразования Лапласа с помощью пакета MathСad.

16. Решение уравнений динамических систем в нормальной форме Коши и определение исходного процесса пакетов MathСad, MathLab.

17. Исследование устойчивости решений систем дифференциальных уравнений по Раусу- Гурвицу в пакетах MathСad, MathLab.

18. Исследование устойчивости решений систем дифференциальных уравнений с помощью характеристического уравнения в пакетах MathСad, MathLab.

Литература:

Гулд Х., Тобочник Я. Компьютерное моделирование в физике. М.: Мир, 1990.

Хеерман Д.В. Методы компьютерного эксперимента в теоретической физике. М.: Наука, 1990.

Фарлоу С. Уравнения с частными производными для научных работников и инженеров. М.: Мир, 1985.

Херхагер М., Партолль Х. MathCad 2000: полное руководство: Пер. с нем. - К.: BHV, 2000.

Потемкин В.Г. MatLab 6: среда проектирования инженерных приложений. М.: Диалог-МИФИ, 2003.

Специальность 38.02.02 Биотехнические и медицинские аппараты и системы

1. Возможности MathCad по исследованию устойчивости решений систем нелинейных ОДУ (на примере задачи устойчивости численности популяции).

2. Решение задачи о росте молодого листа Виктории-регии с помощью пакета MathСad.

3. Решение задачи о размножении бактерий с помощью пакета MathСad.

4. Решение задачи о получении раствора с помощью пакета MathСad.

5. Моделирование эволюционных процессов в пакете MathСad.

6. Решение задачи о радиоактивном распаде с помощью пакета MathСad.

Литература:

Самойленко А.М., Кривошея С.А., Пестюк Н.А. Дифференциальные уравнения: примеры и задачи. М.: Высшая школа, 1989.

Дьяконов В.П. MathCad 2001. Учебный курс. СПб.: Питер, 2001.

Специальность 52.02.01 Технология и оборудование ювелирного производства

1. Контактные задачи. Пластические деформации. Расчёт в программе MathСad.

2. Контактные задачи. Условия разрушения. Расчёт в программе MathСad.

3. Контактные задачи. Текучесть. Расчёт в программе MathСad.

4. Внедрение абсолютно жёсткого штампа в упругую полуплоскость.

5. Дизайн ювелирной шкатулки. Графические программы.

6. Дизайн рекламного проспекта ювелирной фирмы. Corel Draw.

7. Макетирование логотипа и рекламного листка ювелирной мастерской в программе Corel Draw.

8. Моделирование стеллажа для ювелирных изделий в программе 3d-Max.

9. Создание рекламного щита ювелирного магазина в программе Photoshop.

10. Решение дифференциального уравнения колебательного процесса массы в вязкоупругой среде в пакетах MathCad, MathLab.

11. Решение системы дифференциальных уравнений2-х и 3-х массовой системы в вязкоупругой среде в пакетах MathCad, MathLab.

12. Построение эскизов орнаментов их типовых и унифицированных элементов.

13. Моделирование технологического оборудования по методу золотого сечения.

14. Конструирование эскиза технологического оборудования с учетом требований эргономики и антропометрии.

15. Проектирование типовых ювелирных изделий из типовых орнаментов.

16. Моделирование формы ограненного бриллианта.

17. Моделирование формы ограненного самоцветного камня.

18. Движение материального тела (шар, призма) на вязкоупругой основе (имитация полирования).

Литература:

Самойленко А.М., Кривошея С.А., Пестюк Н.А. Дифференциальные уравнения: примеры и задачи. М.: Высшая школа, 1989.

Гулд Х., Тобочник Я. Компьютерное моделирование в физике. М.: Мир, 1990.

Рашевская М.А. CORELDRAW. Практическое руководство.М.: Диалог-МИФИ, 2003.

Миронов Д. CORELDRAW 9. Учебный курс. СПб.: Питер, 1999.

Петерсон М., Ларри М. Эффективная работа с 3D Studio MAX. СПб.: Питер, 1998.

Стразницкас М. Эффективная работа с Photoshop 5. СПб.: Питер, 1999.

Тайц А.М., Тайц А.И. Adobe Illustrator 8. Учебный курс. СПб.: Питер, 1999.

Специальность 38.01.02 Оптико-электронные и лазерные приборы и системы

1. Спектральный анализ функций конечной длительности в пакетах MathCad, MatLab.

2. Спектральный анализ сигналов на основе быстрого преобразования Фурье пакетах MathCad, MatLab.

3. Моделирование свободных колебаний цепочки связанных гармонических осцилляторов пакетах MathCad, MatLab.

4. Моделирование вынужденных колебаний цепочки связанных гармонических осцилляторов пакетах MathCad, MatLab.

5. Модель волновых пакетов, движущихся в среде с дисперсией.

6. Моделирование волновых эффектов интерференции и дифракции.

7. Математические модели распространения света в структурно неоднородных средах.

8. Расчет в среде MathCad пропускной способности оптической системы с амплитудно-стабилизированным передатчиком.

9. Расчет в среде MathCad пропускной способности оптической системы в связи с лазерным передатчиком, работающим ниже порога.

10. Решение задачи о поглощении светового потока с помощью пакета MathCad.

19. Решение задаче о светимости электрической лампочки в пакетах MathCad, MathLab.

20. Решение задачи о скорости химической реакции между веществами в пакетах MathCad, MathLab.

21. Решение задачи о форме зеркала с помощью дифференциальных уравнений в пакетах MathCad, MathLab.

Литература:

Ландау Л.Д., Лифшиц Е,М. Механика. М.: Наука, 1958.

Мандельштам И.Л. Лекции по теории колебаний. М.: Наука, 1972.

Гулд Х., Тобочник Я. Компьютерное моделирование в физике. М.: Мир, 1990.

Гетманова Е.Г., Костарев Д.Б. Резонансные явления в системе связанных осцилляторов// Электромагнитные волны и электронные системы. 2000. т. 6 № 5.

Крауфорд Ф. Волны. М.: Наука, 2000.

Потемкин В.Г. MatLab 6: среда проектирования инженерных приложений. М.: Диалог-МИФИ, 2003.

Дьяконов В.П. MathCad 2001. Учебный курс. СПб.: Питер, 2001.

Специальность 38.02.01 Информационно-измерительная техника

1. Возможности MathCad по решению нелинейных ОДУ (на примере задачи об RLC -контуре с нелинейной индуктивностью).

2. Возможности MathCad по решению нелинейных ОДУ (на примере задачи об RLC -контуре с нелинейной емкостью).

3. Возможности MathCad по решению нелинейных ОДУ (на примере задачи об RLC -контуре с нелинейным сопротивлением).

4. Возможности MathCad по решению ОДУ с периодическими коэффициентами (на примере задачи об RLC -контуре с периодически меняющейся индуктивностью).

5. Возможности MathCad по решению ОДУ с периодическими коэффициентами (на примере задачи об RLC -контуре с периодически меняющейся емкостью).

6. Возможности MathCad по решению ОДУ с периодическими коэффициентами (на примере задачи о параметрическом возбуждении колебаний маятника с переменной длиной).

7. Возможности MathCad по решению систем ОДУ (на примере задачи о 2-х RLC -контурах, связанных через емкость).

8. Возможности MathCad по решению систем ОДУ (на примере задачи о 2-х RLC -контурах, связанных через индуктивность).

9. Возможности MathCad по решению систем ОДУ (на примере задачи о 2-х связанных маятниках).

10. Приложения рядов Фурье к решению простейших задач математической физики.

11. Дифференциальные уравнения механических колебаний.

Литература:

Баскаков С.И. Радиотехнические цепи и сигналы. М.: Высшая школа,1988.

Зоммерфельд А. Электродинамика. М.: ИЛ, 1958.

Тамм И.Е. Основы теории электричества. М.: Наука, 1966.

Кунин С. Вычислительная физика. М.: Мир, 1992.

Херхагер М., Партолль Х. MathCad 2000: полное руководство: Пер. с нем. - К.: BHV, 2000.

Специальность 38.02.03 Техническое обеспечение безопасности

1. Цифровая обработка сигналов, заданных графически.

2. Реализация алгоритма быстрого преобразования Фурье.

3. Специализированный пакет MathCad. Вейвлет-анализ непрерывного сигнала.

4. Специализированный пакет MathCad. Вейвлет-анализ дискретного сигнала.

5. Фурье-анализ дискретного сигнала с использованием пакета MathCad.

6. Фурье-анализ непрерывного сигнала с использованием пакета MathCad.

7. Анализ дискретного сигнала с использованием алгоритма быстрого преобразования Фурье.

8. Современные стандарты защиты информации.

9. Программирование кодировки текстовой информации.

10. Реализация стандартов блочного шифрования (ГОСТ-28147-89, DES, СТБ 1176.1-99).

11. Реализация алгоритмов шифрования с открытым ключом.

12. Стеганографические методы защиты информации.

13. Исследование модели конфигурации структуры охранной системы.

Литература:

Дьяконов В.П., Вейвлеты. От теории к практике, М.: Солон-Р, 2002.

Воробьев В.И., Грибунин В.Г. Теория и практика вейвлет-преобразований. СПб.: ВУС, 1999.

Жуков А.И. Метод Фурье в вычислительной математике. М.: Наука, 1992.

Хеннер Е.К., Шестаков А.П. Математическое моделирование. Пермь: Пермский государственный педагогический университет, 1995.

Мандельштам И.Л. Лекции по теории колебаний. М.: Наука, 1972.

Специальность 41.01.01 Технология материалов и компонентов электронной техники

1. Численное решение краевых задач для уравнений теплопроводности.

2. Численное решение задачи для уравнения диффузии

3. Моделирование фазовых переходов в молекулярной динамике средствами

4. Моделирование колебательных движений в среде Delphi на примере маятника.

5. Моделирование свободного движения тела с высоты в среде Delphi.

6. Решение задаче о светимости электрической лампочки в пакетах MathCad, MathLab.

7. Решение задачи о скорости химической реакции между веществами в пакетах MathCad, MathLab.

8. Решение задачи о радиоактивном распаде с помощью пакета MathCad.

Литература:

Самарский В.А., Введение в численные методы. М.: Наука, 1975.

Марчук Г.И. Методы вычислительной математики. М.: Наука, 1980.

Самойленко А.М., Кривошея С.А., Пестюк Н.А. Дифференциальные уравнения: примеры и задачи. М.: Высшая школа, 1989.

Поршнев С.В. Компьютерное моделирование физических процессов в пакете MatLab. М.: Горячая линия - Телеком, 2003.

Дьяконов В.П. MathCad 2001. Учебный курс. СПб.: Питер, 2001.

Специальность 38.02.04 Спортивная инженерия

1. Разработка приложения в Delphi для работы с БД "Рейтинговая система ATP".

2. Организация БД "Рейтинговая система FIFA" на основе баз данных Internet.

3. Разработка приложения в Delphi для работы с базой данных "Рейтинговая таблица по водным видам спорта"

4. Решение задачи о движении лодки с помощью пакета MathCad.

5. Решение задачи о движении локомотива с помощью пакета MathCad.

6. Решение задачи о движении материальной точки с помощью пакета MathCad.

7. Решение задачи о полете парашютиста с помощью пакета MathCad.

8. Задача о разорении игрока.

9. Моделирование простейших механизмов применяемых в спортивных тренажерах.

Литература:

Самарский В.А. Введение в численные методы. М.: Наука, 1975.

Самойленко А.М., Кривошея С.А., Пестюк Н.А. Дифференциальные уравнения: примеры и задачи. М.: Высшая школа, 1989.

Специальность 54.01.01 Метрология, стандартизация и сертификация

1. Применение средств Microsoft Office в метрологии и сертификации.

2. Решение задач математической статистики с помощью встроенных функций Microsoft Excel.

3. Анализ рекламы в пакете STATISTICA.

4. Методы визуального анализа в пакете STATISTICA.

5. Изучение методов кластерного анализа в пакете STATISTICA

6. Пакет STATISTICA: проведение факторного анализа.

7. Структурные уравнения в пакете STATISTICA.

8. Дисперсионный анализ в пакете STATISTICA.

9. Корреляционный анализ в пакете STATISTICA.

10. Прогнозирование и трендовый анализ.

Литература:

Боровиков В. STATISTICA: искусство анализа данных на компьютере: Питер, 2003.

Корн Г., Корн Т. Статистические методы построения эмпирических формул. М.: Высшая школа, 1988.

Специальность 54.01.02 Методы и приборы контроля качества и диагностики состояния объектов

1. Решение задач математической статистики с помощью встроенных функций Microsoft Excel.

2. Средства обработки эксперимента в STATISTICA.

3. Средства контроля качества в пакете STATISTICA.

4. Оценка эффективности измерительных систем в пакете STATISTICA.

5. Статистический контроль производственного процесса.

Литература:

Боровиков В. STATISTICA: искусство анализа данных на компьютере: Питер, 2003.

Тейлор Дж. Введение в теорию ошибок. М.: Мир, 1985.

Соболь И.М. Численные методы Монте-Карло. М.: Наука, 1973.

Гмурман В.Е. Теория вероятности и математическая статистика. М.: Высшая школа, 1998.

Общие темы работ