Построение модели Хольта-Уинтерса

Для оценки начальных значени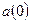й и 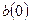применим линейную модель с первыми восьми значениями заданного временного ряда 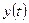(Таблица 2).

Линейная модель имеет вид: 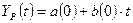. Оценим коэффициенты линейной модел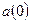и и 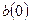с помощью метода наименьших квадратов (МНК).

Таблица 2. Расчёт коэффициентов линейной модели

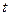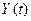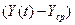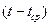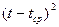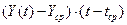Сумма
Среднее значение	4,5	48,5

Определим значения коэффициентов нашей линейной модели по формулам:

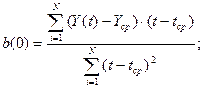
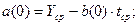
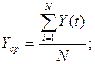
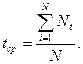
Линейная модель с учетом полученных коэффициентов будет иметь следующий вид:

Из этого уравнения находим расчётные значения 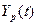и сопоставляем их с фактическими значениями заданного временного ряда (Таблица 3).

Таблица 3. Значения заданного временного ряда и расчетной модели

Т
Y(t)
Yр(t)

Оценим приближенные значения коэффициентов сезонности I – IV кварталов F(-3), F(-2), F(-1) и F(0) для года, предшествующего году, по которому имеются данные.

Адаптивная мультипликативная модель Хольта-Уинтерса имеет вид:

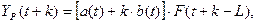
Где k – период упреждения; 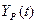- расчетное значение показателя для t -го периода; a(t), b(t) и F(t) – коэффициенты модели; 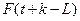- значение коэффициента сезонности того периода, для которого рассчитывается показатель; L – период сезонности (для квартальных данных L =4).

Уточнение (адаптация к новому значению параметра времени t) коэффициентов модели производятся по формулам:

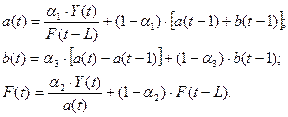
Значения параметров сглаживания, согласно заданию, таковы:

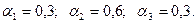
Тогда для момента времени t=0, k=1 имеем:

При моменте времени t=1 имеем:

для t=1, k=1 имеем: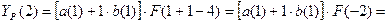

Для момента времени t=2 имеем:

Для t=2, k=1 имеем:

Для момента времени t=3 имеем:

Для t=3, k=1 имеем:

Для момента времени t=4 имеем:

Для t=4, k=1 имеем:

Для момента времени t=5 имеем:

Для t=5, k=1 имеем:

Для момента времени t=6 имеем:

Для t=6, k=1 имеем:

Для момента времени t=7 имеем:

Для t=7, k=1 имеем:

Для момента времени t=8 имеем:

Для t=8, k=1 имеем:

Для момента времени t=9 имеем:

Для t=9, k=1 имеем:

Для момента времени t=10 имеем:

Для t=10, k=1 имеем:

Для момента времени t=11 имеем:

Для t=11, k=1 имеем:

Для момента времени t=12 имеем:

Для t=12, k=1 имеем:

Для момента времени t=13 имеем:

Для t=13, k=1 имеем:

Для момента времени t=14 имеем:

Для t=14, k=1 имеем:

Для момента времени t=15 имеем:

Для t=15, k=1 имеем:

Для момента времени t=16 имеем:

Занесем полученные данные модели Хольта-Уинтерса в таблицу 4.