2015-03-22
424
В математическом анализе правилом Лопита́ля называют метод нахождения пределов функций, раскрывающий неопределённости вида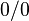 
и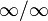 
. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Точная формулировка
Правило говорит, что если функци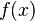и 
и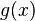 
обладают следующим набором условий:
1. 
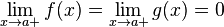или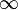 
;
2. 
;
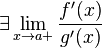3. 
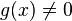в некоторой окрестности точки 
,
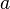тогда существует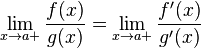 
. При этом теорема верна и для других баз
