Теорема Ферма, - утверждение, что для любого натурального числа n > 2 уравнение xn + yn = zn (уравнение Ферма) не имеет решений в целых ненулевых числах x, y, z.
Теорема 5 (Ролля). Пусть функция f(x) непрерывна на [a,b] и дифференцируема на (a,b), f(a) = f(b). Тогда внутри отрезка существует по крайней мере одна точка c, такая, что f( c ) = 0.
Доказательство. Известно, что непрерывная на отрезке функция достигает своего наибольшего и наименьшего значений. Если оба значения достигаются на концах отрезка, то они равны по условию, а это означает, что функция тождественно постоянна на [a,b]. Тогда производная такой функции равна нулю. Если же хотя бы одно из значений - максимальное или минимальное - достигается внутри отрезка, то производная равна нулю в силу теоремы Ферма.
Геометрический смысл этой теоремы хорошо иллюстрируется на следующем рисунке (рис.23): по теореме Ролля существует хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс, в этой точке производная равна нулю.
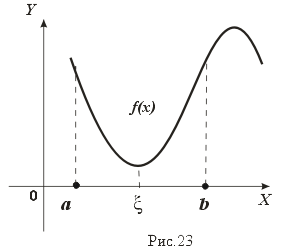
Отметим, что все условия теоремы существенны, при невыполнении хотя бы одного из них утверждение теоремы неверно.
Теорема Ролля является частным случаем теоремы Лагранжа.
Теорема 6 (Лагранжа). Пусть функция f(x) непрерывна на [a,b] и дифференцируема на (a,b). Тогда внутри отрезка существует по крайней мере одна точка c, такая, что
| f' (c) = (f (b) -f (a)) / (b-a). | (8) |
Доказательство. Введем новую функцию
g (x) = f (x) -f (a)-(f (b) -f (a))(x-a) / (b-a).
Эта функция удовлетворяет условиям теоремы Ролля: она непрерывна на [a,b], дифференцируема на (a,b), g(a) = g(b) = 0. Следовательно, найдется точка cÎ (a,b), такая, что
g' (c) = f' (c)-(f (b) -f (a)) / (b-a) = 0.
Отсюда
f' (c) = (f (b) -f (a)) / (b-a).
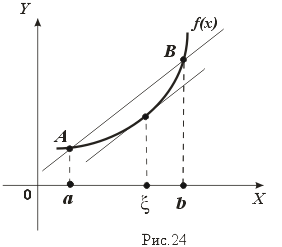
Геометрическая интерпретация теоремы Лагранжа приведена на рис.24. Заметим, что (f(b)-f(a))/(b-a) является угловым коэффициентом секущей, проходящей через точки A(a,f(a)),B(b,f(b)) кривой y = f(x), а f'(c) есть угловой коэффициент касательной к той же кривой, проходящий через точку C(c,f(c)). Из теоремы Лагранжа следует, что на кривой y = f(x) между точками A и B найдется такая точка C, касательная в которой параллельна секущей AB.
Следствие 2. Если производная функции f(x) равна нулю на некотором множестве, то функция тождественно постоянна на этом множестве.
Данное следствие автоматически следует из формулы (8).
Торема 3. (Теорема Коши) Пусть функции f (x) и g (x)
1. непрерывны на отрезке [ a, b ];
2. дифференцируемы в интервале (a, b);
3. " x Î (a, b) g '(x) ≠ 0.
4. Если дополнительно потребовать, чтобы g (a) ≠ g (b), то условие g' (x) ≠ 0 можно заменить менее жестким: 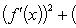
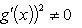
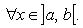
Тогда существует точка c Î (a, b) такая, что
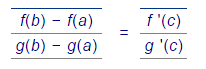 | (3) |
Формула (3) называется формулой Коши.
 2015-03-22
2015-03-22 1364
1364
