Рекуррентные соотношения

Рассмотрим обобщение последовательностей Фибоначчи. Формула

u_{n + r} = c₁ u_{n + r – 1} + c₂ u_{n + r – 2} + ∙ ∙ ∙ + c_r u_n

называется однородным линейным рекуррентным уравнением порядка r.

Ее решением является последовательность {u_n}, однозначно определенная начальными значениями u₀, u₁, u₂, ∙ ∙ ∙, u_{r –1} . Решение такого уравнения называется возвратной или рекуррентной последовательностью порядка r.

Пример 1. Геометрическая прогрессия является решением уравнения u_n+1=qu_n. Ее члены описываются формулой u_n= u₀qⁿ. Отсюда геометрическая прогрессия является возвратной последовательностью порядка 1.

Пример 2. Арифметическая прогрессия u_n = u₀ + nd удовлетворяет соотношению u_n+1 - u_n = u_n+2 - u_n+1. Получаем однородное рекуррентное уравнение u_n+2 = 2u_n+1 - u_n. Начальные данные задаются значениями u₀ и u₁=u₀+d. Отсюда арифметическая прогрессия является возвратной последовательностью порядка 2.

Пример 3. Произвольная периодическая последовательность является возвратной последовательностью порядка p, удовлетворяющей рекуррентному соотношению u_{n + p}=u_n. Здесь p – период последовательности.

Для заданного рекуррентного уравнения

u_{n + r} = c₁ u_{n + r – 1} + c₂ u_{n + r – 2} + ∙ ∙ ∙ + c_r u_n

найдем производящую функцию 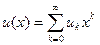возвратной последовательности { u_n }. Обозначим K(x)=1- c₁x - c₂x² - ∙ ∙ ∙ - c_rx^r.

Теорема 1. Произведение u(x)K(x) = D(x) является многочленом степени < r.

Доказательство. Вычислим коэффициент ряда D(x) при x^{n+ r} . Он при n ≥ 0 будет равен u_{n + r} - (c₁ u_{n + r – 1} + c₂ u_{n + r – 2} + ∙ ∙ ∙ + c_r u_n) = 0. Отсюда D(x) – многочлен степени < n.