Контрольные работы 1 курс 2 семестр
Контрольная работа №3
Векторный анализ
Задача 1. Найти векторные линии в векторном поле 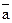 .
.
1.1. 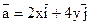
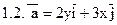
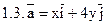
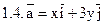
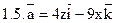
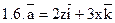
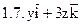
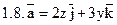
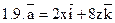
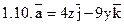
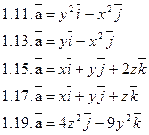
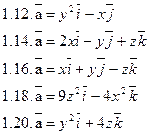
Задача 2. Найти поток векторного поля 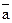 через часть плоскости Р, расположенную в первом октанте (нормаль образует острый угол с осью Dz).
через часть плоскости Р, расположенную в первом октанте (нормаль образует острый угол с осью Dz).
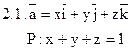
| 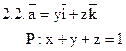
|
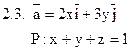
| 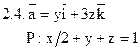
|
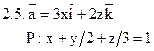
| 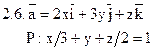
|
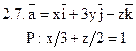
| 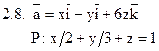
|
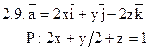
| 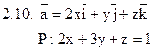
|
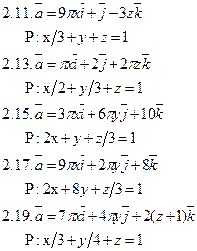
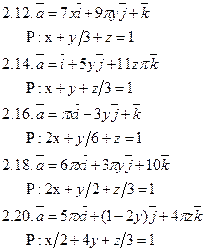
Задача 3. Найти поток векторного поля 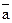 через замкнутую поверхность S (нормаль внешняя).
через замкнутую поверхность S (нормаль внешняя). 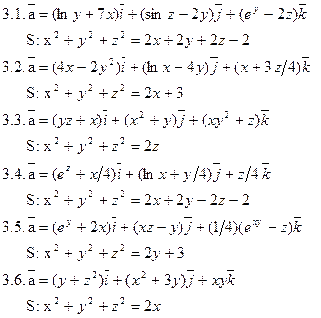
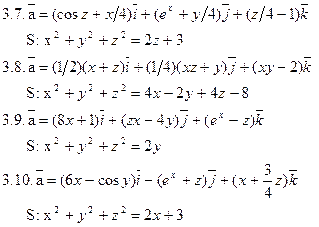
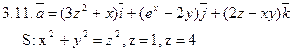
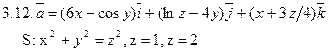
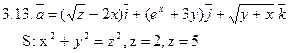
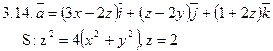
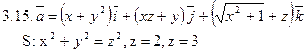
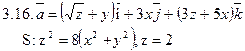
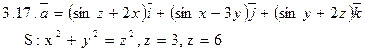
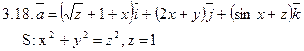
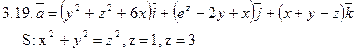
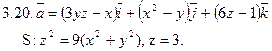
Задача 4. Найти работу силы 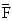 при перемещении вдоль отрезка MN от точки M к точке N.
при перемещении вдоль отрезка MN от точки M к точке N.
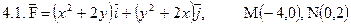

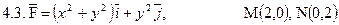
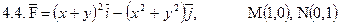

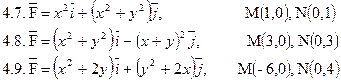
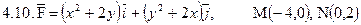
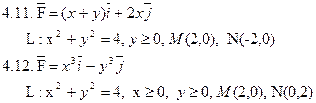
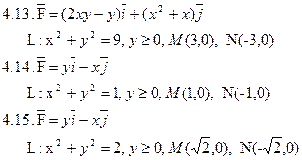
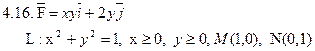
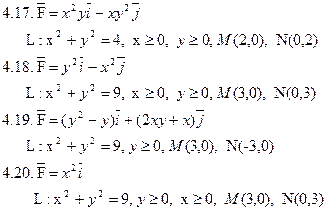
Числовые ряды
5.Доказать непосредственно (по определению) сходимость следующих рядов и вычислить их суммы:
5.1. 1 – ½ + 1/4-1/8+…+(-1)n-1/2n-1+…
5.2. (1/2+1/3)+(1/22+1/32)+…(1/2n+1/3n)+…
5.3. ½+3/22+5/23+…+2n-1/2n+…
5.4. 1/1*2+1/2*3+…+1/n(n-1)+…
5.5. 1/1*4+1/4*7+…+1/(3n-2)*(3n+1)+…
5.6. 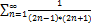
5.7. 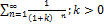
5.8. 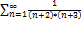
5.9. 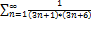
5.10. 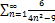
5.11. 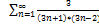
5.12. 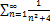
5.13. 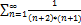
5.14. 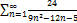
5.15. 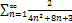
5.16. 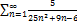
5.17. 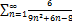
5.18. 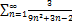
5.19. 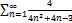
5.20. 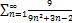
6. Исследовать на сходимость числовые ряды
6.1. 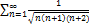
6.2. 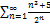
6.3. 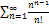
6.4. 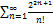
6.5. 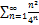
6.6. 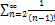
6.7. 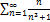
6.8. 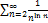
6.9. 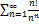
6.10. 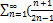 )n
)n
6.11. 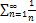
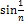
6.12. 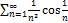
6.13. 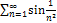
6.14. 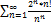
6.15. 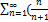 )n
)n
6.16. 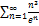
6.17. 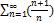 n
n
6.18. 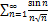
|
|
|
6.19. 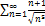
6.20. 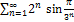
7.Исследуйте на сходимость следующие ряды:
7.1. 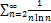
7.2. 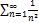
7.3. 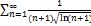
7.4. 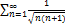
7.5. 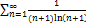
7.6. 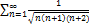
7.7. 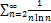
7.8. 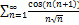
7.9. 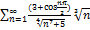
7.10. 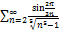
7.11. 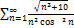
7.12. 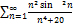
7.13. 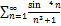
7.14. 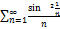
7.15. 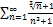
7.16. 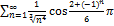
7.17. 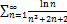
7.18. 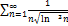
7.19. 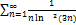
7.20. 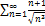
8.Исследовать на абсолютную и условную сходимость следующие знакочередующиеся ряды:
8.1. 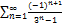
8.2. 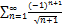
8.3. 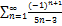
8.4. 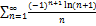
8.5. 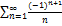
8.6. 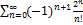
8.7. 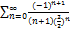
8.8. 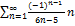
8.9. 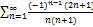
8.10. 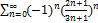
8.11. 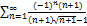
8.12. 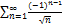
8.13. 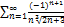
8.14. 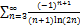
8.15. 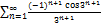
8.16. 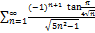
8.17. 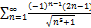
8.18. 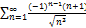
8.19. 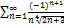
8.20. 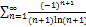
9.Определить область сходимости функционального ряда и исследовать на сходимость на границе области сходимости следующие функциональные ряды:
9.1. 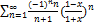
9.2. 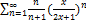
9.3. 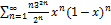
9.4. 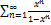
9.5. 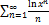
9.6. 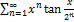
9.7. 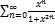
9.8. 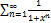
9.9. 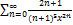
9.10. 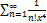
9.11. 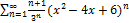
9.12. 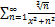
9.13. 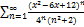
9.14. 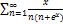
9.15. 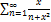
9.16. 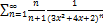
9.17. 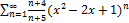
9.18. 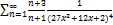
9.19. 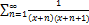
9.20. 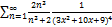
10. Найти радиус и интервал сходимости. Исследовать на сходимость на концах интервала:
10.1. 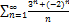 (
(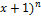
10.2. 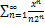
10.3. 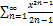
10.4. 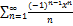
10.5. 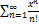
10.6. 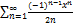
10.7. 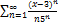
10.8. 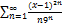
10.9. 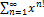
10.10. 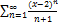
10.11. 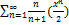
10.12. 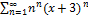
10.13. 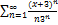
10.14. 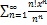
10.15. 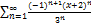
10.16. 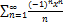
10.17. 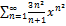
10.18. 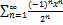
10.19. 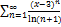
10.20. 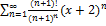
11. Разложить следующие функции в ряд Маклорена. Найти их интервал сходимости:
11.1. y= 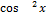
11.2. y= 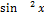
11.3. y= 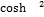 x
x
11.4. y= 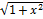
11.5. y=(x- 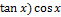
11.6. y=x 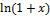
11.7. y= 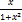
11.8. y= 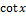
11.9. y= 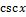
11.10. y= 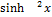
11.11. y= 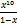
11.12. y= (1+X) 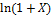
11.13. y= 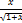
11.14. y= (1+ 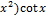
11.15. y= 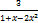
11.16. y= 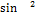 x
x 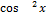
11.17. y= 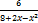
11.18. y= 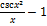
11.19. y= (3+ 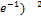
11.20. y= (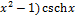
12. Вычислить интеграл с точностью до 0,001:
12.1. 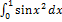
12.2. 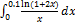
12.3. 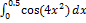
12.4. 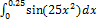
12.5. 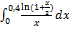
12.6. 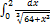
12.7. 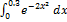
12.8. 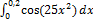
12.9. 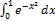
12.10. 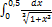
12.11. 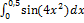
12.12. 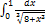
12.13. 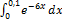
12.14. 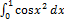
12.15. 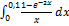
12.16. 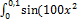 )
) 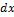
12.17. 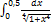
12.18. 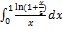
12.19. 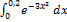
12.20. 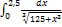
13. Разложить в ряд Фурье функции с периодом 2π:
13.1. ƒ(x)= π2-x2; x€ 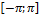
13.2. ƒ(x)= 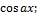 x€
x€ 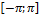
13.3. ƒ(x)= 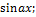 x€
x€ 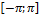
13.4. ƒ(x)= 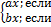 -π
-π 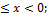
0 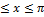
13.5. ƒ(x)= 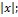 x€
x€ 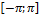
13.6. ƒ(x)= 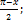 x€
x€ 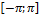
13.7. ƒ(x)=  x€
x€ 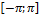
13.8. ƒ(x)= 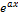 ; x€
; x€ 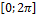
13.9. ƒ(x)=x 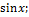 x€
x€ 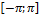
13.10. ƒ(x)=x 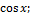 x€
x€ 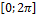
13.11. ƒ(x)= 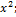 x€
x€ 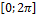
13.12. ƒ(x)= 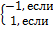 -π
-π 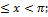
0 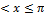
13.13. ƒ(x)= 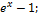 x€
x€ 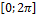
13.14. ƒ(x)= 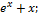 x€
x€ 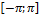
13.15. ƒ(x)= 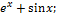 x€
x€ 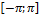
13.16. ƒ(x)= 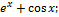 x€
x€ 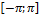
13.17. ƒ(x)= 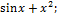 x€
x€ 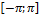
13.18. ƒ(x)= x- 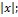 x€
x€ 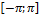
13.19. ƒ(x)= 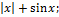 x€
x€ 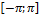
13.20. ƒ(x)= 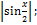 x€
x€ 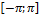
 2015-03-22
2015-03-22 386
386







