2015-03-22
352
В России при расчете по банковским операциям используется, в основном, формула сложного банковского процента. Однако при расчете по потребительским кредитам используется формула простых процентов. Приведем несколько примеров расчетов размера периодических выплат по потребительским кредитам.
а) Погашение кредита равными долями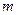 
раз в году. Пусть кредит в размере 
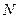рублей выдан на 
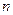лет под 
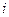простых годовых процентов и погашаться будет равными выплатами 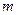раз в году. Определим размер этих выплат. Всего должно быть выплачено 
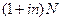рублей. Количество платежей равно 
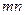. Следовательно, каждый платеж составит
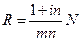рублей.
Определим банковскую ставку сложного процента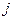 
, эквивалентную этой схеме погашения долга. Получаем, что номинальная величина кредита 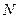должна быть равна приведенной величине ренты с выплатой 
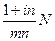под 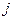процентов годовых:
.
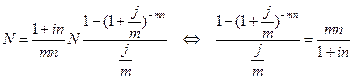Это уравнение можно решить приближенно, при помощи таблиц коэффициентов приведения годовой ренты. В частности, при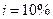 
, 
, 
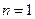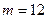получаем:
.
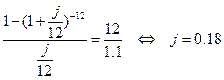Следовательно, при данной схеме выплат 10-процентный кредит эквивалентен 18-процентному банковскому кредиту.
|
|
|
б) Правило 78. При этой схеме первоначальная сумма кредита 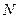выплачивается равными долями, а проценты на кредит в общей сумме 
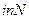погашаются выплатами, уменьшающимися в арифметической прогрессии. Пусть кредит в размере 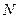рублей предоставлен на 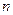лет, число платежей равно 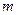раз в году, годовая процентная ставка равна 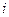. Тогда платежи по процентам за кредит составят:
.
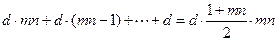Из соотношения
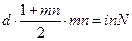
получаем:
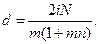
При 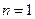, 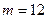(ежемесячные выплаты) получаем
,
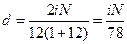то есть выплаты по процентам каждый месяц уменьшаются на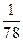 
долю.
