Примеры. №1. Решить методом Рунге – Кутта дифференциальное уравнение при начальном условии у(0) = 1 на отрезке [0; 0,5] с шагом 0,1

№1. Решить методом Рунге – Кутта дифференциальное уравнение 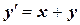при начальном условии у ( 0 ) = 1 на отрезке [0; 0,5] с шагом 0,1.

Решение.

Для i = 0 вычислим коэффициенты k_i:

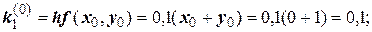
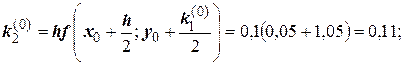
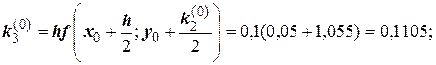
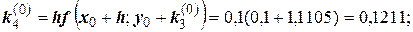
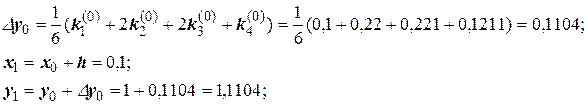
Последующие вычисления приводить не будем, а результаты представим в виде таблицы.

i	xi	k	Dyi	yi
			0,1000	0,1104
	0,1100
	0,1105
	0,1211
	0,1		0,1210	0,1325	1,1104
	0,1321
	0,1326
	0,1443
	0,2		0,1443	0,1569	1,2429
	0,1565
	0,1571
	0,1700
	0,3		0,1700	0,1840	1,3998
	0,1835
	0,1842
	0,1984
	0,4		0,1984	0,2138	1,5838
	0,2133
	0,2140
	0,2298
	0,5		1,7976

№2. Решим предыдущий пример методом Эйлера.

Решение.

Применяем формулу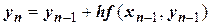

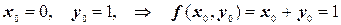
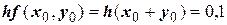
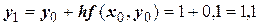
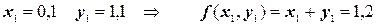
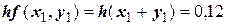
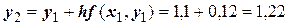
Производя аналогичные вычисления далее, получаем таблицу значений:

i
xi	0,0	0,1	0,2	0,3	0,4	0,5
yi		1,1	1,22	1,362	1,528	1,721

Применим теперь уточненный метод Эйлера (точность 0,001).

i
xi	0,0	0,1	0,2	0,3	0,4	0,5
yi		1,111	1,243	1,400	1,585	1,799

Для сравнения точности приведенных методов численного решение данного уравнения решим его аналитически и найдем точные значения функции у на заданном отрезке.

Уравнение 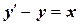является линейным неоднородным дифференциальным уравнением первого порядка. Решим соответствующее ему однородное уравнение.

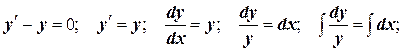
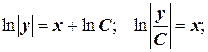
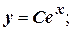
Решение неоднородного уравнения имеет вид .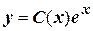

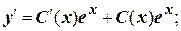
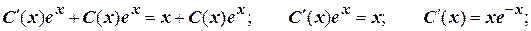
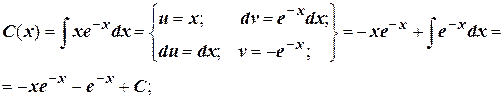
Общее решение: .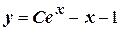

C учетом начального условия: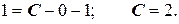

Частное решение: .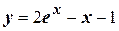

Для сравнения полученных результатов составим таблицу.

i	xi	yi
Метод Эйлера	Уточнен-ный метод Эйлера	Метод Рунге-Кутта	Точное значение
	0,1	1,1	1,111	1,1104	1,1103
	0,2	1,22	1,243	1,2429	1,2428
	0,3	1,362	1,4	1,3998	1,3997
	0,4	1,528	1,585	1,5838	1,5837
	0,5	1,721	1,799	1,7976	1,7975

Как видно из полученных результатов метод Рунге – Кутта дает наиболее точный ответ. Точность достигает 0,0001. Кроме того, следует обратить внимание на то, ошибка (расхождение между точным и приближенным значениями) увеличивается с каждым шагом вычислений. Это обусловлено тем что, во-первых, полученное приближенное значение округляется на каждом шаге, а во-вторых – тем что, в качестве основы вычисления принимается значение, полученное на предыдущем шаге, т.е. приближенное значение. Таким образом, происходит накопление ошибки.

Это хорошо видно из таблицы. С каждым новым шагом приближенное значение все более отличается от точного.

Варианты заданий

№11.1. Решить с помощью методов Эйлера, уточненного метода Эйлера, Рунге-Кутта и аналитически следующие дифференциальные уравнения при заданных начальных условиях, на заданном отрезке с шагом 0,2. Сравнить полученные результаты.

№ варианта	Уравнение	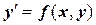Начальные условия (x 0, y 0)	Отрезок [ x 0, xк ]
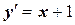		x 0= –1, y 0= 0	[–1, 1]
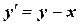		x 0= 0, y 0= 2	[0, 2]
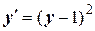		x 0= 1, y 0= 0	[1, 3]
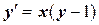		x 0= 0, y 0= 2	[0, 2]
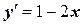		x 0= 0, y 0= 2	[0, 2]
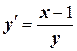		x 0= 1, y 0= 1	[1, 3]
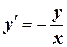		x 0= 1, y 0= 1	[1, 3]
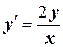		x 0= 1, y 0= 2	[1, 3]
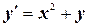		x 0= 0, y 0= 2	[0, 2]
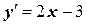		x 0= 2, y 0= 0	[2, 4]
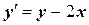		x 0= 0, y 0= 3	[0, 2]
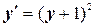		x 0= –3, y 0= –2	[–3, –1]
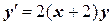		x 0= –2, y 0= 1	[–2, 0]
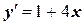		x 0= –3, y 0= 5	[–3, –1]
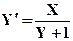		X0= - 4,Y0= 4	[-4,-2]
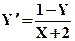		X0= 2,Y0= 2	[2,- 4]
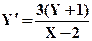		X0= 3,Y0= 0	[3,5]
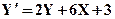		X0= 0,Y0= -2	[0,2]
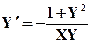		X0= -3,Y0= 1	[-3,-1]
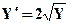		X0= 2,Y0= 9	[2,4]
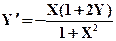		X0= -2,Y0= -0.4	[-2,0]
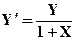		X0= - 4,Y0= -2	[-4,-2]
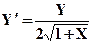		X0= 0,Y0= 2	[0,2]
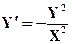		X0= 1,Y0= 1	[1,3]

Контрольные вопросы

1. Когда применяются численные методы решения дифференциальных уравнений?

2. Перечислите известные вам численные методы решения дифференциальных уравнений.

3. В чем заключается суть метода Эйлера?

4. В чем смысл уточненного метода Эйлера?

5. В чем смысл метода Рунге-Кутта?

6. Как рассчитать погрешность вычислений в приближенных методах?