Закон контрапозиции

На основе данного сложного высказывания А®В можно сформулировать обратное ему высказывание B®A. Нетрудно убедиться, что оно не равносильно исходному.

Для всякого сложного высказывания A®B можно сформулировать противоположное 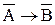. Нетрудно убедиться, что оно не равносильно исходному.

Высказывание типа 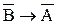называется обратно – противоположным.

Нетрудно убедиться, что оно равносильно исходному:

.

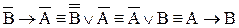Такая равносильность называется законом контрапозиции [25].

Согласно этому закону:

1) высказывания A®B и 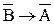одновременно истинны либо одновременно ложны;

2) высказывание, которое является обратно противоположной данной теореме A®B также является теоремой (здесь сложное высказывание называется теоремой);

3) вместо данной теоремы можно доказать обратно противоположную ей теорему.

Кроме того, если высказывание A®B – теорема, то A есть достаточное условие B, а B – необходимое условие A.

Если оба высказывания являются теоремами (A®B, B®A; т.е. A«B), то A – необходимое и достаточное условие B, а B – необходимое и достаточное условие A.

Если A®B – теорема, а B®A не теорема, то A – достаточное, но не необходимое условие B, а B – необходимое, но не достаточное условие A.