Цель: расширить и углубить знания студентов по цепям синусоидального тока.
Задача: научить применять полученные знания для расчета цепей.
Векторной диаграммой называется совокупность векторов на комплексной плоскости, изображающих синусоидальные функции времени одинаковой частоты и построенных с соблюдением их взаимной ориентации по фазе.
Как было показано выше, в основе комплексного метода лежит замена синусоидальных функций вращающимися векторами (рис. 3.3). Однако попытка нарисовать вектор, вращающийся на комплексной плоскости в течение какого-либо интервала времени, приведет к появлению на ней зачерненной окружности (сектора). Поэтому на векторных диаграммах условились рисовать векторы для момента времени 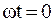 (т.е. по сути делать “мгновенную фотографию” вращающихся векторов при
(т.е. по сути делать “мгновенную фотографию” вращающихся векторов при 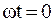 ) – рис. 3.6.
) – рис. 3.6.
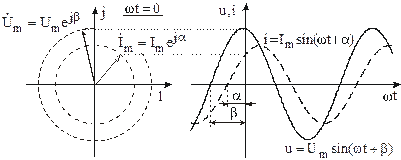
Рис. 3.6
Векторные диаграммы дают наглядное представление о фазовых соотношениях между токами и напряжениями на отдельных участках электрической цепи. Так, в рассматриваемом примере рис. 3.6 напряжение опережает ток. Это приводит к тому, что на векторной диаграмме (рис. 3.6) вектор напряжения повернут в положительном направлении (т.е. против часовой стрелки) относительно вектора тока, причем угол между рассматриваемыми векторами меньше 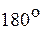 . Учет этих двух факторов (поворот одного вектора относительно другого в положительном направлении и угол между векторами, меньший
. Учет этих двух факторов (поворот одного вектора относительно другого в положительном направлении и угол между векторами, меньший 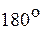 ) позволяет с помощью векторных диаграмм легко определять опережающие (отстающие) напряжения и токи.
) позволяет с помощью векторных диаграмм легко определять опережающие (отстающие) напряжения и токи.
|
|
|
Так, на векторной диаграмме рис. 3.7 ток 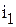 опережает ток
опережает ток 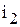 .
.
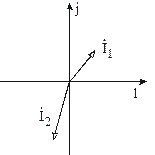
Рис. 3.7
С помощью векторных диаграмм можно производить сложение и вычитание синусоидальных функций времени, что позволяет осуществлять геометрическую интерпретацию законов Кирхгофа на комплексной плоскости.
Рассмотрим в качестве примера сложение двух синусоидальных токов.
Дано: 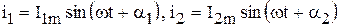 .
.
Определить 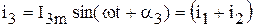 .
.
Отложим на комплексной плоскости векторы 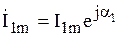 и
и 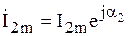 (рис. 3.8).
(рис. 3.8).
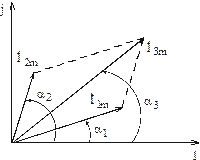
Рис. 3.8
Геометрическая сумма векторов 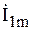 ,
, 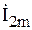 дает комплексную амплитуду искомого тока
дает комплексную амплитуду искомого тока 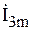 . Длина полученного вектора равна амплитуде искомого тока
. Длина полученного вектора равна амплитуде искомого тока 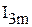 , а угол между действительной осью и суммарным вектором равен начальной фазе
, а угол между действительной осью и суммарным вектором равен начальной фазе 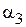 тока
тока 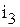 . Отметим, что в рассматриваемом примере ток
. Отметим, что в рассматриваемом примере ток 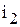 опережает токи
опережает токи 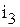 и
и 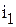 .
.
Рассмотрим векторные диаграммы токов и напряжений для отдельных пассивных элементов цепи.
 2015-03-27
2015-03-27 903
903








