2015-03-27
499
Лекция 4
Вернёмся к общему случаю
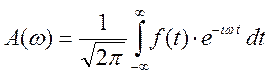
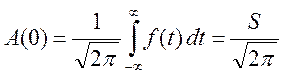
Пусть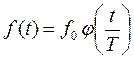 
, 
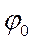- амплитуда, Т – характерная ширина
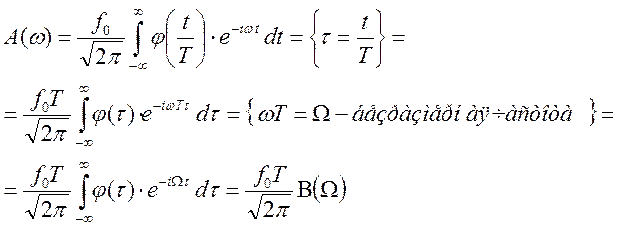
Рассмотрим теперь гладкую функцию
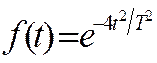(18)
- распределение Гаусса
 |
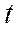
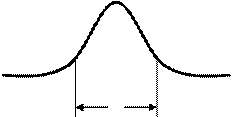T
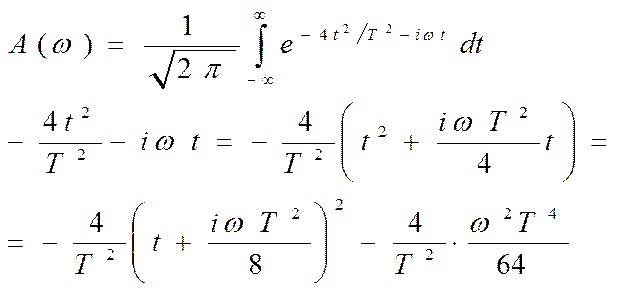
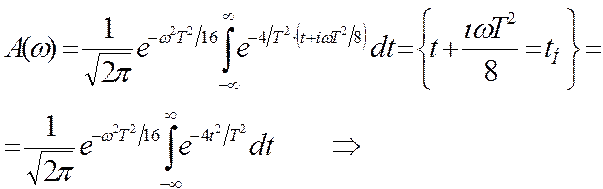
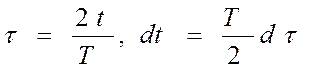
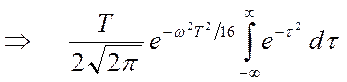
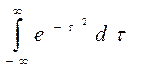- это число
Этот интеграл вычислить проще из двукратного интеграла
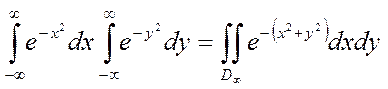
в полярных координатах
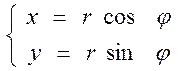
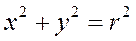
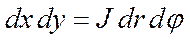
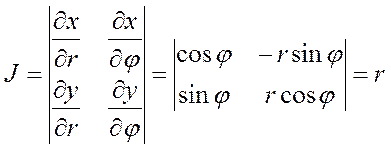
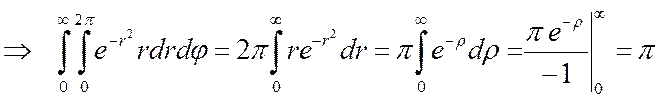
Тогда,
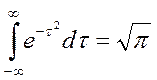
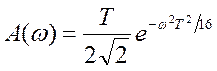Итак:
Нужно обратить внимание, что:
- форма спектра повторяет форму сигнала
- при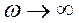 
получаем экспоненциальную
(а не степенную) асимптотику
Текущий спектр
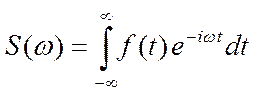(19)
В случае реального процесса мы знаем функцию f(t)
на конечном интервале, поэтому на самом деле, нужно вводить текущий спектр
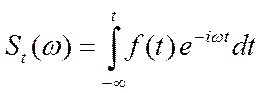или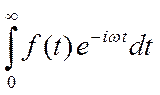 
Если сигнал начался в t0 , то с него и нужно начинать отсчёт.
Построим текущий спектр синусоиды
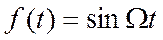
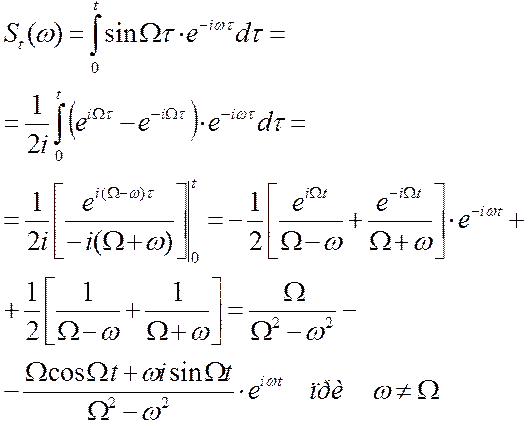
Через полпериода:
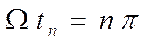
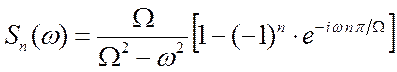
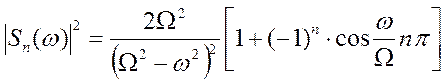
Нули: n – чётность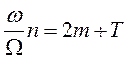 
n – нечётность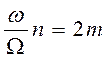 
При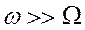 
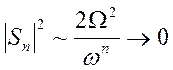
Наибольшая величина при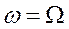 
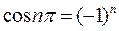, получаем 
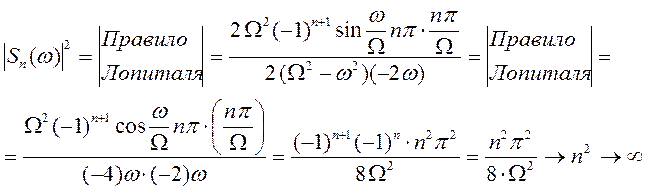
как и положено.
Отсюда видно, что спектральный максимум формируется со временем. И если мало время усреднения, то спектр может сильно отличаться от реального.
Теорема Котельникова (1933г.)
|
|
|
Если спектр функции ограничен, то f(t) представима счётным количеством своих значений.
Пример:
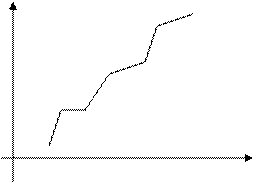f(t) Если f(t) - набор ломаных,
то ясно, что нужно знать
счётное количество
значений.
t
Теорема. Любую функцию f(t), спектр которой ограничен fС, можно представить набором чисел, следующих друг за другом через 1/[2 fС ]
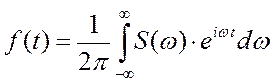(20)
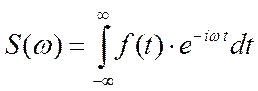
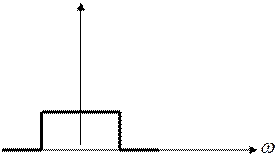
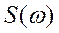Спектр ограничен,
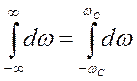поэтому:
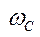
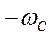
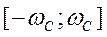
Полоса частот
Функция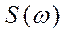 
на конечном интервале частот.
Эта теорема устанавливает возможность сколь угодно точного восстановления мгновенных значений сигнала с ограниченным спектром исходя из отсчётных значений (выборок), взятых через равные промежутки времени.
