У задачи линейного программирования в канонической форме все ограничения (кроме требования неотрицательности переменных) имеют вид равенств, т.е.
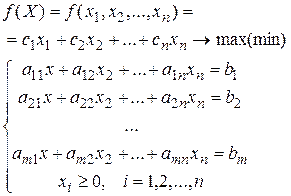
| или 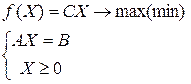 , (1.1) , (1.1)
|
где  - вектор переменных,
- вектор переменных, 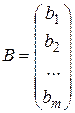 - столбец свободных членов,
- столбец свободных членов, 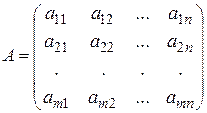 - матрица системы ограничений.
- матрица системы ограничений.
Задачей линейного программирования в симметричной форме записи называется задача вида (в матричной форме записи):
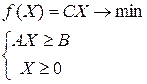 или
или 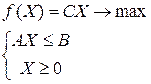 (1.2)
(1.2)
1.2. Симплекс-метод или метод улучшенного плана – один из универсальных методов решения задач линейного программирования. Это упорядоченный процесс перехода от одного опорного плана к другому, при котором (при решении задач на максимум) соответствующие значения целевой функции возрастают (или, по крайней мере, не убывают).
Пусть задача линейного программирования имеет канонический вид
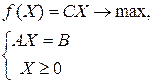 , (1.3)
, (1.3)
причем столбец свободных членов удовлетворяет условию B³0. В системе ограничений m уравнений и n неизвестных, т.е. матрица A имеет размер m´n,вектор-столбец B – m´1, вектор-строка коэффициентов целевой функции C – 1´n. Алгоритм решения задачи (3.1) симплекс-методом будем сопровождать решением конкретного примера, а именно задачи
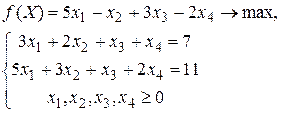 (1.4)
(1.4)
1) Получение начального опорного плана. Один из вариантов – преобразование расширенной матрицы системы ограничений к приведенному виду, выделение базисных и свободных переменных:
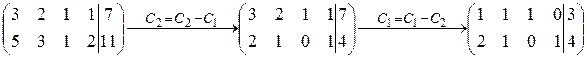 .
.
Здесь x3, x4 – базисные переменные, x1, x2 – свободные переменные. При преобразованиях необходимо следить за тем, чтобы столбец свободных членов оставался неотрицательным. Начальный опорный план получается, если присвоить свободным переменным значения, равные нулю; при этом базисные переменные принимают значения, равные числам в соответствующей строке столбца свободных членов: Xоп1=(0;0;3;4).
2) По преобразованной системе ограничений составляют симплекс-таблицу. В верхней строке (заголовки столбцов) располагаются свободные переменные, в крайнем левом столбце – базисные переменные; крайний правый столбец – это столбец свободных членов, а самая нижняя строка является строкой целевой функции (об определении чисел D1, D2, Df в этой строке речь пойдет ниже). Остальное содержимое таблицы – столбцы преобразованной матрицы, отвечающие соответствующим столбцам свободных переменных (см. таблицу 1.1).
| x1 | x2 | B | x1 | x2 | B | |||
| x3 | x3 | |||||||
| x4 | x4 | |||||||
| f | D1 | D2 | Df | f | -6 | |||
| Таблица 1.1. | Таблица 1.2 |
Для того чтобы найти значение DI (в рассматриваемом примере i=1,2), воспользуемся правилом: вектор из коэффициентов при базисных переменных в целевой функции скалярно умножить на i -й столбец симплекс-таблицы и вычесть из найденного числа коэффициент целевой функции при соответствующем свободном переменном. Для Df скалярно перемножаются вектор коэффициентов при базисных переменных целевой функции и столбец свободных членов:
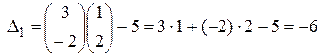 ;
;
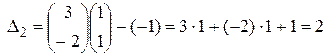 ;
;
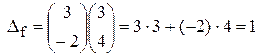 .
.
Итак,таблица 1.2 представляет собой окончательный вид первой симплекс-таблицы.
Замечание. Следует обратить внимание на то, что Df – это значение целевой функции при найденном начальном опорном решении: Df=f(0,0,3,4)=1. Числа же D1, D2 – оценки, которые будут учитываться при проверке этого решения на оптимальность.
3) Построенное начальное опорное решение является оптимальным, если все оценки DI неотрицательны (причем в случае положительности всех оценок решение единственно!). Если среди этих оценок есть отрицательная, но среди чисел в ее столбце нет положительных, то исходная задача не имеет решения в силу неограниченности целевой функции. Наконец, если в каждом столбце с отрицательной оценкой есть хотя бы один положительный элемент, то необходимо осуществить переход к новому опорному плану (который затем снова проверяется на оптимальность).
4) Переход к новому опорному плану проводится по следующей схеме.
- Выбирается ведущий столбец (столбец с отрицательной оценкой). Если отрицательных оценок несколько, то выбирается столбец с отрицательной оценкой, наибольшей по модулю. В рассматриваемом примере ведущим будет первый столбец (D1=-6)
- Выбирается ведущая строка. Для этого определяется наименьшее из симплексных отношений (т.е. отношений свободных членов к соответствующим положительным элементам ведущего столбца). В примере оба числа в первом столбце положительны, поэтому: 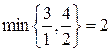 , ведущей будет вторая строка.
, ведущей будет вторая строка.
- На пересечении ведущих строки и столбца определяется ведущий (разрешающий) элемент (в примере это 2, соответствующая ячейка таблицы 3.2 заштрихована).
- В заголовках меняются местами переменные, соответствующие ведущим строке и столбцу (в примере меняются местами x1 и x4).
- Ведущий элемент заменяется значением, обратным этому элементу (в примере ½).
- Все остальные элементы ведущей строки делятся на ведущий элемент, а все остальные элементы ведущего столбца делятся на ведущий элемент, взятый со знаком «-» (см. таблицу 1.3, в которую внесены описанные выше изменения, а не найденные пока числа заменены греческими буквами).
- Оставшиеся элементы находят с помощью «правила многоугольника» 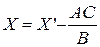 (здесь Х – вычисляемое значение,
(здесь Х – вычисляемое значение, 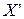 - соответствующий элемент «старой» таблицы, B – ведущий элемент, A и C – оставшиеся вершины четырехугольника с диагональю
- соответствующий элемент «старой» таблицы, B – ведущий элемент, A и C – оставшиеся вершины четырехугольника с диагональю 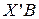 ). Для разбираемого примера имеем:
). Для разбираемого примера имеем:
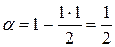 ;
; 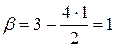 ;
; 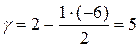 ;
; 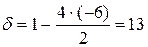 .
.
Итак, получена новая симплекс-таблица (таблица 1.4), которая определяет новое опорное решение (свободные переменные x2, x4; их значения будут равны нулю; базисные переменные x1, x3; их значения – соответствующие числа из столбца свободных членов: x1=2, x3=1). Значение функции на этом опорном решении – в правом нижнем углу, т.е. Xоп2=(2;0;1;0), f(2,0,1,0)=13.
| x4 | x2 | B | x4 | x2 | B | |||
| x3 | -1/2 | α | β | x3 | -1/2 | ½ | ||
| x1 | ½ | ½ | x1 | ½ | ½ | |||
| f | g | d | f | |||||
| Таблица 1.3 | Таблица 1.4 |
5) Построенное новое опорное решение требуется снова проверить на оптимальность и, если необходимо, повторить операцию перехода. В рассматриваемой задаче, однако, все оценки стали положительными, и, следовательно, Xоп2=(2;0;1;0)=Xоптим, fmax=f(2,0,1,0)=13.
Замечание 1. Задачи, в которых решается задача на минимум, легко свести к рассмотренному случаю. Для этого, сохранив систему ограничений, исследуем задачу с целевой функцией 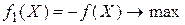 .
.
Замечание 2. Бывают ситуации (например, когда система ограничений несовместна), когда начальное опорное решение построить невозможно; в этом случае исходная задача не имеет решения.
 2015-03-27
2015-03-27 480
480








