2.1. Постановка задачи и математическая модель транспортной задачи. Предположим, что существуют N потребителей и M поставщиков некоторого однородного груза, у каждого из поставщиков определенный запас этого груза (Ai единиц, i=1,2,…,M), а каждому из потребителей требуется Bj единиц груза (j=1,2,…, N). Известны также затраты cij на перевозку единицы груза от поставщика Ai к потребителю Bj. Требуется составить такой план перевозок от поставщиков к потребителям, чтобы суммарные затраты на перевозки оказались минимальными (при этом должны быть по возможности вывезены все запасы поставщиков и удовлетворены все запросы потребителей).
В случае, когда суммарные запасы совпадают с суммарными запросами, задача называется задачей с правильным балансом, а ее модель - закрытой. В противном случае говорят о задаче с неправильным балансом и об открытой модели. Существуют специальные приемы приведения открытой модели к закрытой (они будут рассмотрены позже).
Данные транспортной задачи обычно записываются в виде таблицы, заголовки строк которой содержат информацию о запасах, заголовки столбцов – информацию о запросах, а в нижнем правом углу каждой ячейки указывается стоимость перевозки единицы груза (затраты на перевозку единицы груза).
При составлении математической модели через xij обозначается количество единиц груза, который будет перевезен от поставщика Ai к потребителю Bj (объем перевозок от Ai к Bj). Эти значения будут вноситься в центр соответствующей ячейки.
С учетом сказанного целевая функция принимает вид
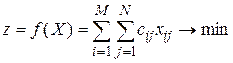
(просуммированы все произведения затрат на соответствующий объем перевозок). Ограничения связаны с вывозом запасов и удовлетворением запросов, поэтому математическая модель имеет вид:
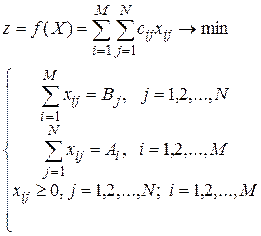
| Пример 2.1. Транспортная задача задана с помощью таблицы 2.1, из которой видно, что на складах трех поставщиков A1, A2, A3 сосредоточены соответственно 30, 190 и 250 единиц груза, потребители B1, B2, B3, B4 нуждаются соответственно в 70, 120, 150, 130 единицах груза, а стоимости перевозок указаны непосредственно в таблице. |
|
Таблица 2.1.
Заметим, что суммарные запасы (30+190+250=470) равны суммарным запросам (70+120+150+130=470). Разместим в основной (незаштрихованной) части таблицы искомые объемы перевозок xij и перейдем к составлению математической модели. Заметим, что нумерация соответствует привычной нумерации элементов в матрицах (i – номер строки, j – номер столбца). Итак, целевая функция принимает вид
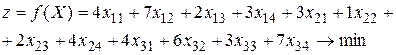 (2.1)
(2.1)
(просуммировали произведения стоимостей на объемы перевозок по всем строкам). При построении системы ограничений сначала суммируем объемы перевозок по каждому столбцу (удовлетворяем все запросы), а потом суммируем объемы перевозок по каждой строке (вывозим все запасы). Учтем также неотрицательность значений xij и получаем следующие условия:
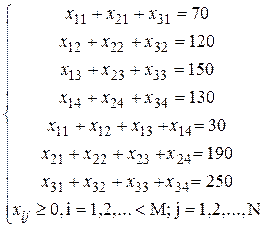 (2.2)
(2.2)
Итак, мы построили математическую модель предложенной задачи с целевой функцией (2.1) и системой ограничений (2.2).
Транспортная задача сводится к задаче линейного программирования, однако для ее решения существуют специальные алгоритмы. При этом сначала задача сводится к закрытой, затем строится начальное решение, а затем оно оптимизируется с помощью метода потенциалов.
Задание 2.2. Решить транспортные задачи (определить оптимальное значение целевой функции).
1)
| 2)
|
3)
| 4)
| ||||||||||||||||||||||||||||||||||||||||||||||||||
5)
| 6)
| ||||||||||||||||||||||||||||||||||||||||||||||||||
7)
| 8)
| ||||||||||||||||||||||||||||||||||||||||||||||||||
9)
| 10)
|
 2015-03-27
2015-03-27 921
921








