Интерполирование периодических функций, заданных экспериментальными данными

Задача аппроксимации периодической функции и с помощью тригонометрического интерполяционного многочлена формулируется следующим образом. Пусть на отрезке [а,b] задана функция у=f(х) значениями у₁,...,у_N в точках х₁,..„х_N, причём эта функция является периодической с периодом
T=b-a. По экспериментальным данным необходимо найти неизвестные коэффициенты a_k, b_k тригонометрического многочлена:

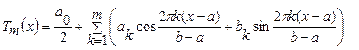,(4.59)

таким образом, чтобы:

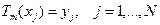, (4.60)

где N -целое нечетное число.

Сначала будем предполагать, что функция у=f(х) задана на отрезке [0,2π], тогда тригонометрический многочлен имеет вид:

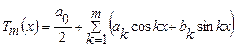. (4.61)

Коэффициенты тригонометрического многочлена можно найти путём решения системы линейных алгебраических уравнений (4.61). Эта система может иметь решение (в обычном смысле) только в том случае, когда выполняется условие N=2m+1.

Если число N является чётным, т.е. N=2m, то приближение для функции y=f(x) имеет вид:

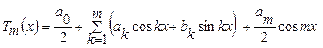; (4.62)

где

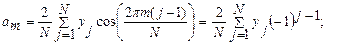
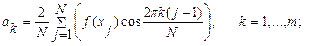
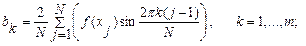
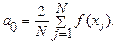
Пусть по определению:

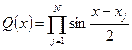. (4.63)

Тогда получим формулу аналогичную формуле Лагранжа:

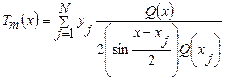. (4.64)

Рассмотрим некоторые частные случаи выбора узлов, позволяющих значительно упростить формулу (4.64):

1) Пусть N=2m+1 и х_j являются нулями полинома:

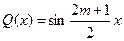; (4.65)

тогда

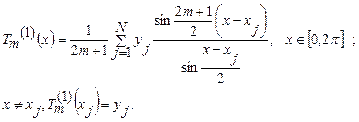(4.66)

2) Eсли узлами интерполяции являются нули полинома:

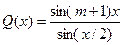, (4.67)

то .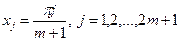

Тогда:

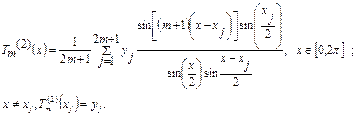(4.68)

3) Аналогично можно показать, что если функция у=f(х) задана на отрезке [0,2π], то имеют место соотношения:

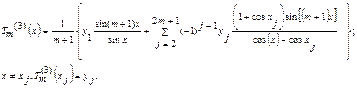(4.69)

где y_j -значения функции у=f(х) в точках:

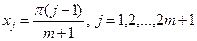. (4.70)