На практике для аппроксимации функций часто используется интерполяционный полином Ньютона. Этот полином вводится с помощью разделенных разностей различных порядков, найденных по значениям функции y1,...,уN в точках x1,...,xN.
По определению разделенные разности 1-го порядка равны:
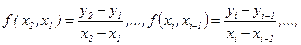
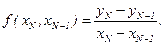 (4.36)
(4.36)
Разности 2-го порядка определяются с помощью разностей 1-го порядка:
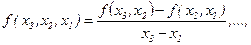 (4.37)
(4.37)
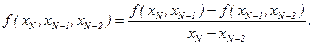
Пусть найдены разности (n -1)-го порядка. Тогда разности n-го порядка можно вычислить по формуле:
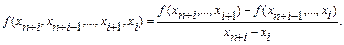 (4.38)
(4.38)
Разделенные разности располагаются в специальной таблице, которая строится по следующей схеме:
х1 у1
f(x2,x1)
х2 у2
f(x3,x2) f(x3,x2,x1)
х3 у3 f(x4,x3,x2,x1)
………………………… f(x4,x3) f(x4,x3,x2) f(x5,x4,x3,x2,x1)
х4 у4 ………………………………… f(x5,x4,x3,x2)……….
……………………… f(x5,x4) f(x5,x4,x3)
х5 у5
Каждое число этой таблицы равно частному от деления разностей двух смежных с ним чисел в столбце слева, на разность хi, соответствующих тем уi, которые лежат на диагоналях, проходящих через это число.
Разделенные разности n-го порядка можно представить в виде [4,7,16,22]
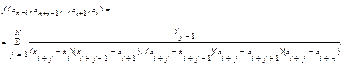 (4.39)
(4.39)
Отсюда следует, что разделенная разность является симметричной функцией относительно узлов х„ т.е. не зависит от порядка расположения входящих в нее переменных х,.
Теперь перейдем к построению интерполяционного полинома Ньютона. Пусть х - произвольная точка отрезка [а,b]. Рассмотрим разность 1-го порядка:
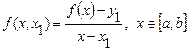 . (4.40)
. (4.40)
Из этого выражения можно найти значение функции в точке 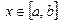 :
:
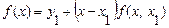 . (4.41)
. (4.41)
Разность 2-го порядка имеет вид:
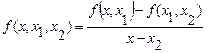 (4.42)
(4.42)
Отсюда:
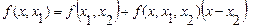 .(4.43)
.(4.43)
Подставив это выражение в (4.41), получим:
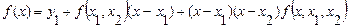 . (4.44)
. (4.44)
Аналогично разность 3-го порядка:
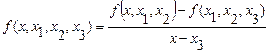 . (4.45)
. (4.45)
позволяет представить (4.44) в виде
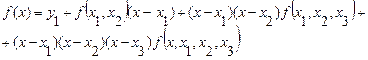 .(4.46)
.(4.46)
Продолжая процесс подстановки, получим выражение:
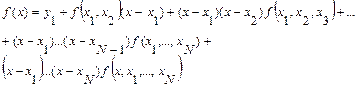 , (4.47)
, (4.47)
которое можно переписать в следующей форме:
f(x) = PN-1(x) + RN-1(x), (4.48)
где
Pn-1(x) = y1 + (x-x1)f(x1,x2) +...+ (x-x1)...(x-xN-1)f(x1,...,xN), (4.49)
Rn-1(x) = (x-x1)...(x-xN)f (x,x1,...,xN). (4.50)
Полином Pn-1(x) является интерполяционным, так как имеют место равенства
f(хj) = PN-1(xj), j = 1,...,N. (4.51)
Этот полином обычно называется интерполяционным полиномом Ньютона, a Rn-1(x) - остаточным членом формулы Ньютона. Так как по значениям функции в некоторых точках можно построить единственный интерполяционный полином, то полином Ньютона путем перегруппировки его членов можно преобразовать в интерполяционный полином Лагранжа и наоборот. Однако, в отличие от интерполяционного полинома Лагранжа, для которого каждое из слагаемых суммы (4.16) зависит от всех узлов интерполяции, произвольный m -й член полинома Ньютона зависит только от т первых узлов. Поэтому для полинома Ньютона добавление новых узлов интерполяции приводит лишь к появлению новых слагаемых полинома, без изменения первоначальных.
Остаточный член формулы Ньютона (4.50) представляет собой истинную погрешность метода интерполирования. Если известно, что функция f(x) N раз непрерывно дифференцируема, то:
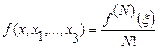 , (4.52)
, (4.52)
где ξ — некоторая точка отрезка [ а,b ], а остаточный член:
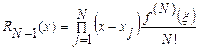 . (4.53)
. (4.53)
На практике производные функции f(x) обычно известны и поэтому остаточный член часто оценивается непосредственно по формуле (4.50).
Если все узлы интерполяции являются равноотстоящими, т.е. xi = x1+ (i- 1) h, то разделенные разности имеют вид:
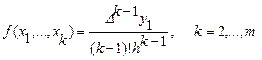 , (4.54)
, (4.54)
где
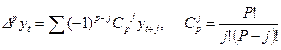
Отсюда следует, что интерполяционную формулу Ньютона можно представить в следующем виде:
. 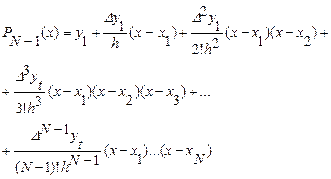 . (4.55)
. (4.55)
В результате мы получим интерполяционную формулу, которая называется интерполяционной формулой Ньютона интерполирования вперед. Эта формула имеет наибольшую точность в начале таблицы.
На практике часто используется интерполяционный полином Ньютона, представленный в несколько иной форме. Так как при построении интерполяционного полинома Ньютона порядок расположения узлов не играет роли, то формулу (4.49) можно представить в виде
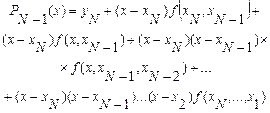 (4.56)
(4.56)
Если узлы хj являются равноостоящими, то из формулы (4.56) получим формулу Ньютона интерполирования назад [20]:
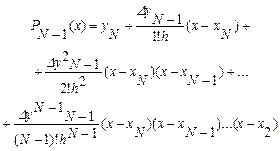 (4.57)
(4.57)
которая имеет наибольшую точность в конце таблицы.
При построении интерполяционных полиномов Ньютона можно использовать таблицу разностей, каждый элемент которой
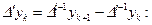
х1 у1
∆ у1
х2 у2 ∆2у1 (4.58)
∆ у2
х3 у3
……………………………………..∆N-1y1
……………………………………………….
……………………… ∆2у1………..∆2уN-2
хN уN
В формуле (4.55) используется верхняя (нисходящая) строка этой таблицы, а в формуле (4.53) - нижняя (восходящая) строка таблицы.
Рассмотрим пример применения интерполяционного полинома Ньютона при обработке экспериментальных данных.
Аппроксимируем с помощью формулы Ньютона интерполирования вперед зависимость тяга несущего винта вертолета Ми-6 от высоты висения у земли. Для построения интерполяционного полинома второй степени выбираем значения тяги в трех точках. Значения тяги и высоты заданы в таблице 1.2.
Таблица 1.2.
| j | |||
| Hj, м | |||
| Tj, m | 35.9 |
Строим таблицу разностей вида (4.58)
5 39
3,1
15 35,9 2,2
0,9
25 35
Тогда формула интерполирования вперед имеет вид
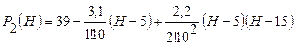 .
.
После элементарных преобразований получим:
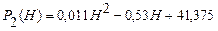 .
.
Очевидно, что в узлах интерполяции 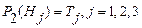 . Вычисления показали, что погрешность аппроксимации в других точках не превышает 150кг.
. Вычисления показали, что погрешность аппроксимации в других точках не превышает 150кг.
Кроме рассмотренных выше методов интерполяции функций, в современной вычислительной математике имеется много различных методов решения интерполяционных задач. Среди них в первую очередь следует выделить методы построения интерполяционных формул Гаусса, Стерлинга и Бесселя и т.д. Достаточно подробное изложение теории интерполяции, а также примеры аппроксимации можно найти в работах [20].
 2015-03-27
2015-03-27 1257
1257
