Теорема Геделя

Одним из наиболее глубоких достижений математики XX века яв­ляется теорема Геделя, которую можно сформулировать следующим образом:

Не существует в рамках данной логической системы такой совокупности аксиом, которая была бы одновременно полна и непротиворечива.

Это означает, во-первых, что на уровне данного языка описания, принадлежащего некоторой логической системе, и опираясь только на базовые высказывания (аксиомы), невозможно сформулировать (или вывести) все производные истинные высказывания (теоремы) - для этого неизбежно необходим некоторый метаязык, - а во-вторых, что концепция любой системы базируется на высшем по отношению к ин­струментарию логическом уровне. Это касается и любой научной кон­цепции; так инструментарий НЛП относится к третьему логическому уровню (стратегии), а концепция - к четвертому. Здесь возможно лишь «горизонтальное» развитие - «вертикальная» эволюция требует пере­хода к новому концептуальному базису. То же можно сказать и о со­временной официальной медицине, имеющей инструментарий не вы­ше третьего логического уровня («Как?», «Каким образом?»), но, главным образом, на втором логическом уровне («Что происходит?», «Что делать?»), что приводит к исключению личности врача из процесса лечения), а концептуальный базис - отчасти, на четвертом логическом уровне(«Почему?», но очень редко «Зачем?»), отчасти на третьем.

Доказательство теоремы Геделя требует глубоких знаний в облас­ти математики и находится за пределами рассматриваемых нами про­блем, поэтому мы ограничимся некоторыми примерами и пояснениями и далее укажем, каким образом она связана с концепцией логических уровней сознания и методами нелинейного мышления, используемыми в структурной психосоматике.

Смысл теоремы Геделя вкратце сводится к следующему: если в рамках некоторой логической системы известны правила вывода, то мы можем установить и определенные базовые высказывания (аксиомы), на основании которых строятся производные высказывания (теоремы). Оказывается, однако, что если используемый нами набор аксиом непро­тиворечив (т. е. может порождать только истинные теоремы), всегда существует множество других истинных теорем, которые никаким ло­гическим путем из указанных аксиом выведены быть не могут, но, тем не менее, будут истинными. Если же мы добавим такие аксиомы, кото­рые позволяют вывести эти истинные теоремы, то набор аксиом стано­вится противоречивым.

Простейшим примером может служить геометрия. Аксиомы Евкли­да непротиворечивы, но они неполны. Спорной аксиомой является ак­сиома параллельных - через точку, лежащую вне данной прямой, можно провести одну и только одну прямую, параллельную данной, т. е. такую, которая не имеет с данной прямой ни одной общей точки. В XIX веке усилиями Лобачевского, Бояи и Римана были высказаны две альтерна­тивные аксиомы: 1) через точку, лежащую вне данной прямой, можно провести более одной прямой, параллельной данной, и 2) через точку, лежащую вне данной прямой, нельзя провести ни одной прямой, парал­лельной данной.

Было очевидно, что, во-первых, аксиома Евклида[25] резко ограничи­вает возможности вывода истинных теорем геометрии, и, во-вторых, неэвклидовые аксиомы параллельных противоречат ей. Противоречие было снято в рамках метатеории, которая включала в себя геометрию Евклида и неэвклидовые геометрии как частные случаи.

То же можно сказать о ньютоновой механике и Специальной тео­рии относительности Эйнштейна - последняя является по отношению к первой метатеорией, поскольку релятивистские эффекты становятся пренебрежимо малы при относительных скоростях наблюдателя и на­блюдаемого тела много меньших скорости света.

На основании сказанного мы упрощенно можем представить себе ситуацию следующим образом: некоторые наборы аксиом (а₁ a₂, а₃, а₄) порождают области выводимых из них теорем, причем некоторые тео­ремы оказываются в области противоречий (для наборов а₁ а₂ и а₃), а некоторые - невыводимы из противоречивого набора а₄; метасистема (метатеория) со своим метаязыком позволяет вывести все истинные теоремы и различить системы аксиом (а₁ а₂, а₃, а₄), которые являются ее частными случаями (рис. 28).

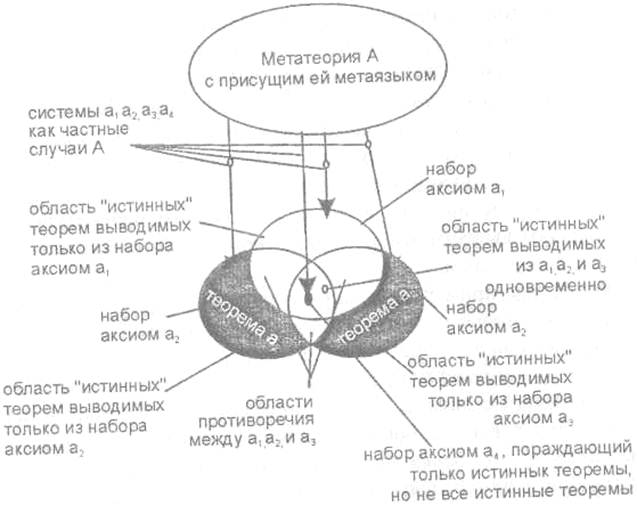
Рис. 28. Теория и метатеория

При этом следует помнить, что сама метатеория, располагающаяся на следующем (высшем) уровне описания по отношению к теории, не может обладать собственной одновременно полной и непротиворечи­вой системой аксиом - для создания такой необходима мета-мета­теория с мета-метаязыком и т. д. (рис. 29). Таким образом, метатеория является обобщением теории, а метаязык - обобщением языка.

Сказанное имеет прямое отношение к понятию логических уров­ней сознания. Действительно, если мы рассматриваем некоторый кон­текст (жизненную ситуацию) на первом логическом уровне, то в поле нашего внимания оказываются только точечные проявления (факты), причем не все, поскольку от нас скрыта динамика происходящего, относящаяся к способу отражения второго логического уровня; точно так же на втором логическом уровне нам недоступна динамика, связанная с нашей собственной личностью, и т. д.

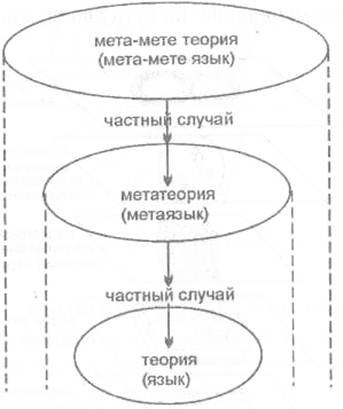
Рис. 29. Метатеории как обобщение

Таким образом, мы можем ввести еще одно определение нелогиче­ского уровня сознания. Это:

некоторая операционная система отражения-отреагирования, наделенная собственным языком описания; она является частным случаем (следствием) некоторой метасистемы, наделенной собст­венным метаязыком, и может порождать подчиненную субсистему, наделенную субъязыком, как собственное следствие (частный случай). Языком первого логического уровня являются факты, второго - про­цессы, третьего - стратегии, четвертого - карты, пятого - космограмма, шестого — глобальное взаимодействие. О языке седьмого ло­гического уровня мы не можем составить вербализованного пред­ставления, поскольку не имеем необходимого для этого метаязыка.

Напомним, что инструментарий каждого следующего уровня со­держит в качестве подчиненного инструментарий всех предыдущих Уровней (рис. 30).

Проведем теперь беглый обзор методов и приемов мышления, рас­сматриваемых структурной психосоматикой как методологией теории познания, в качестве самостоятельных классификационных единиц.

Линейное мышление может быть представлено как способ уста­новления некоторой цепочечной последовательности в рамках логиче­ской системы, установление взаимного расположения в причинно-следственном «пространстве» рассматриваемых инструментарных структур - фактов, процессов, карт и т. д. Нелинейное мышление, на­против, рассматривает структуру более высокого порядка и совокуп­ность всех включенных в нее подчиненных феноменов - процесс как увязку фактов в динакмике, карту как базис стратегий и т. д. Таким образом, нелинейное мышление, по сути своей, многофакторно.

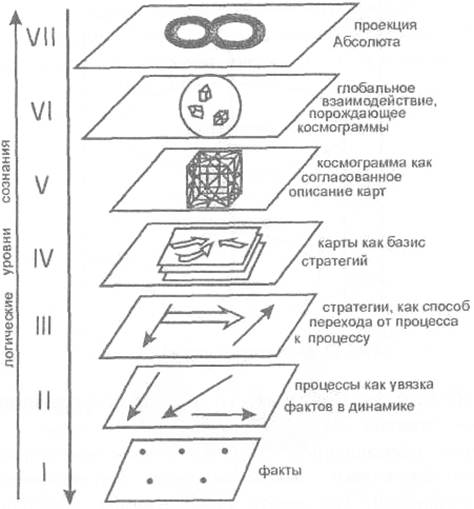
Рис. 30. Метаязыки, как инструментарий логических уровней сознания

Дискурсивное мышление рассматривает полюсные проявления реально­сти и занимается анализом их особенностей. Экскурсивное мышление стре­мится снять полюсность и обозреть противоположности с единой точки зре­ния. (Так выявляются - дискурсивно - магнитные полюса и на их базе стро­ится геодезическая сеть Земли, далее - экскурсивно - выясняется, что эти полюса есть проявления единого магнитного поля и т. п.)

Очевидно, что инструментарий высших логических уровней экскурсивен и нелинеен по отношению к инструментарию подчиненных; однако он и сам содержит дискурсивные и линейные черты по отношению к собственному метауровню (рис. 31).

Далее мы увидим, что следует различать обобщение в рамках од­ного и того же способа отражения-отреагирования (переход от маг­нитных полюсов к магнитному полю) и принципиальную нелиней­ность (переход от стратегий к картам).

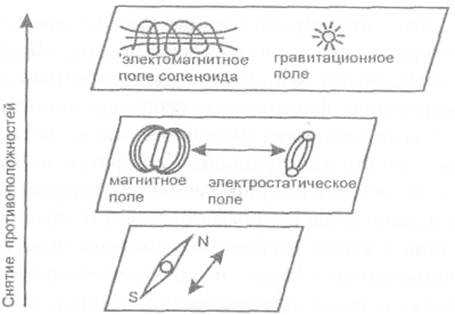
Рис. 31. Снятие полюсов (обобщение)