Рассмотрим некоторую n - местную 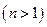 частичную функцию
частичную функцию 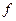 . Допустим, что существует какой - либо «механизм» для вычисления значений функции
. Допустим, что существует какой - либо «механизм» для вычисления значений функции 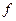 , причём значение функции
, причём значение функции 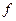 тогда и только тогда неопределённое, когда этот механизм работает бесконечно, не выдавая определённого результата.
тогда и только тогда неопределённое, когда этот механизм работает бесконечно, не выдавая определённого результата.
Фиксируем какие-нибудь значения 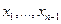 для первых
для первых 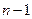 аргументов функции
аргументов функции 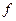 и рассмотрим уравнение
и рассмотрим уравнение
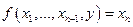 . (1)
. (1)
Чтобы найти натуральное решение 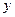 этого уравнения, будем вычислять при помощи нашего «механизма» последовательно значения
этого уравнения, будем вычислять при помощи нашего «механизма» последовательно значения 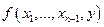 для значений
для значений 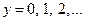 .
.
Наименьшее значение 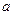 , для которого получится равенство:
, для которого получится равенство: 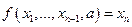 , обозначим следующим образом:
, обозначим следующим образом:
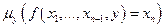 . (2)
. (2)
Описанный процесс нахождения значений выражения (2) будет продолжаться бесконечно в следующих случаях:
а) значение 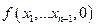 не определено;
не определено;
б) значения 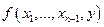 для
для 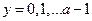 определены, но отличны от
определены, но отличны от 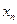 , а значение
, а значение 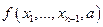 не определено.
не определено.
в) значения 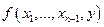 определены для всех
определены для всех 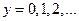 и отличны от
и отличны от 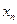 .
.
Во всех этих случаях значение выражения (2) считается неопределённым. В остальных случаях описанный процесс обрывается и дает наименьшее решение 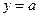 уравнения (1). Это решение является значением выражения (2).
уравнения (1). Это решение является значением выражения (2).
Например, мы уже ввели операцию усечённой разности:
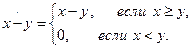
Поэтому, по определению символа 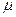 , для всех
, для всех 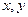 имеем
имеем 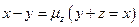 .
.
Аналогично 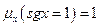 ,
, 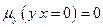 .
.
Значение выражения 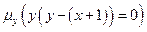 – неопределенное, т.к. уже значение терма
– неопределенное, т.к. уже значение терма 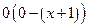 - неопределенное, хотя уравнение
- неопределенное, хотя уравнение 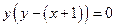 имеет решение
имеет решение 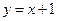 .
.
Этот пример показывает, что для частичных функций 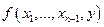 выражение (2) строго говоря, не есть наименьшее решение уравнения (1). Если функция
выражение (2) строго говоря, не есть наименьшее решение уравнения (1). Если функция 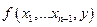 всюду определённая и уравнение (1) имеет решение, то (2) есть наименьшее решение для (1).
всюду определённая и уравнение (1) имеет решение, то (2) есть наименьшее решение для (1).
Значение выражения (2) при заданной функции 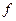 зависит от выбора значений параметров
зависит от выбора значений параметров 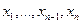 и потому оно является частичной функцией от аргументов
и потому оно является частичной функцией от аргументов 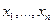 x1. Эту функцию обозначим:
x1. Эту функцию обозначим: 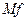 , где
, где 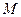 символ операции, переводящей функцию
символ операции, переводящей функцию 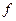 в
в 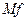 .
.
Если функция 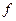 – одноместная, то функцию
– одноместная, то функцию 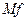 обозначают
обозначают 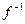 и называют обратной функцией. Таким образом,
и называют обратной функцией. Таким образом, 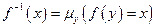 .
.
Для многоместных функций 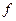 запись
запись 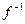 не употребляется. Оператор
не употребляется. Оператор 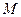 называют оператором минимизации. Например, из записи
называют оператором минимизации. Например, из записи 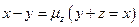 следует, что
следует, что 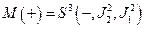 .
.
Определение: Частичная функция 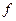 называется частично рекурсивной относительно системы частных функций
называется частично рекурсивной относительно системы частных функций 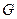 , если
, если 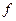 может быть получена из функций системы
может быть получена из функций системы 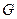 и простейших функций
и простейших функций 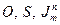 конечным числом операций подстановки, примитивной рекурсии и минимизации.
конечным числом операций подстановки, примитивной рекурсии и минимизации.
Частичная функция 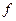 называется частично рекурсивной, если она может быть получена из простейших функций
называется частично рекурсивной, если она может быть получена из простейших функций 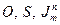 конечным числом операций подстановки, примитивной рекурсии и минимизации.
конечным числом операций подстановки, примитивной рекурсии и минимизации.
Таким образом, частичная рекурсия 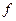 называется частично рекурсивной, если она является значением операторного терма, записанного с помощью операторных символов
называется частично рекурсивной, если она является значением операторного терма, записанного с помощью операторных символов 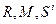 и символов
и символов 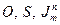 простейших функций.
простейших функций.
Из определения вытекают следующие свойства частично рекурсивных функций:
1)Каждая частичная функция, примитивно рекурсивная относительно системы функций 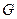 , являются и частично рекурсивной относительно
, являются и частично рекурсивной относительно 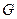 . В частности, все примитивно рекурсивные функции частично рекурсивны.
. В частности, все примитивно рекурсивные функции частично рекурсивны.
2)Класс частично рекурсивных функций шире класса примитивно рекурсивных функций, так как все примитивно рекурсивные функции всюду определённые, а среди частично рекурсивных функций встречаются и функции, не всюду определенные, например 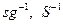 и даже нигде не определенная функция
и даже нигде не определенная функция 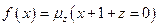 .
.
3)Операции подстановки, примитивной рекурсии и минимизации, произведенные над функциями, частично рекурсивными относительно системы 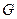 , дают в результате функции, снова частично рекурсивные относительно
, дают в результате функции, снова частично рекурсивные относительно 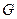 .
.
Чтобы получить представление о связи между примитивно рекурсивными и частично рекурсивными функциями, введем следующие понятия.
Характеристической функцией 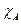 какого-нибудь множества натуральных чисел
какого-нибудь множества натуральных чисел 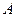 называется одноместная функция, равная
называется одноместная функция, равная 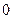 в точках множества
в точках множества 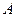 и равная
и равная 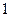 в точках, не принадлежащих
в точках, не принадлежащих 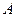 . Частичной характеристической функцией множества
. Частичной характеристической функцией множества 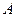 называется функция, равная
называется функция, равная 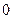 в точках множества
в точках множества 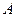 и не определённая в точках, не принадлежащих
и не определённая в точках, не принадлежащих 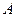 .
.
Например, характеристическая функция пустого множества есть функция, равная 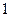 для всех натуральных чисел, а частичная характеристическая функция пустого множества есть нигде не определенная функция.
для всех натуральных чисел, а частичная характеристическая функция пустого множества есть нигде не определенная функция.
Вообще, характеристическая и частичная характеристическая функции совпадают лишь для множества всех натуральных чисел.
Множество натуральных чисел 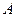 называется примитивно рекурсивным, если его характеристическая функция примитивно рекурсивна. Множество
называется примитивно рекурсивным, если его характеристическая функция примитивно рекурсивна. Множество 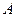 называется частично рекурсивным, если его частичная характеристическая функция частично рекурсивна. Аналогично определяются понятия примитивно рекурсивного и частично рекурсивного множества относительно системы функций
называется частично рекурсивным, если его частичная характеристическая функция частично рекурсивна. Аналогично определяются понятия примитивно рекурсивного и частично рекурсивного множества относительно системы функций 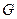 .
.
Теорема 1: Каждое (относительно) примитивно рекурсивное множество является (относительно) частично рекурсивным.
Доказательство: Действительно, пусть 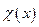 - характеристическая функция какого-нибудь множества натуральных чисел
- характеристическая функция какого-нибудь множества натуральных чисел 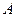 . Тогда функция
. Тогда функция 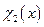 , определяемая равенством
, определяемая равенством 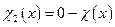 , будет частичной характеристической функцией множества
, будет частичной характеристической функцией множества 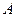 , так как операция вычитания частично рекурсивна, то и функция
, так как операция вычитания частично рекурсивна, то и функция 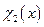 также частично рекурсивна.
также частично рекурсивна.
Теорема 2: Пусть 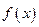 - произвольная примитивно рекурсивная функция и
- произвольная примитивно рекурсивная функция и 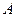 - любое примитивно рекурсивное множество натуральных чисел. Тогда частичная функция
- любое примитивно рекурсивное множество натуральных чисел. Тогда частичная функция 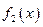 , определённая схемой:
, определённая схемой:
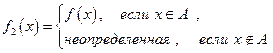 ,
,
является частично рекурсивной.
Доказательство: В самом деле, по теореме 1, частичная характеристическая функция 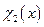 множества
множества 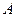 частично рекурсивна. Но по определению функции
частично рекурсивна. Но по определению функции 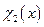 для всех значений
для всех значений 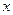 имеет место равенство
имеет место равенство 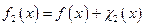 и, значит, функция
и, значит, функция 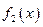 - частично рекурсивна.
- частично рекурсивна.
Доказанная теорема позволяет строить многочисленные примеры частично рекурсивных функций.
Понятие частично рекурсивной функции - одно из главных понятий теории алгоритмов.
С одной стороны, каждая частично рекурсивная функция вычислима путем определённой процедуры механического характера, которая отвечает нашему интуитивному представлению об алгоритмах. С другой стороны, какие бы классы точно очерченных алгоритмов до сих пор фактически ни строились, во всех случаях неизменно оказывалось, что числовые функции, вычислимые посредством алгоритмов этих классов, были частично рекурсивными.
Поэтому общепринятой является следующая естественно научная гипотеза.
Тезис Чёрча. Класс алгоритмически вычислимых частичных числовых функций совпадает с классом всех частично рекурсивных функций.
Тезис Чёрча доказать нельзя, т.к. не существует строгого определения понятия вычислимой функции.
Обобщением тезиса Чёрча является тезис Тьюринга.
Тезис Тьюринга: Класс функций, алгоритмически вычислимых относительно какой-нибудь функции 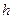 (или класса функций
(или класса функций 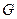 ), совпадает с классом частичных функций, частично рекурсивных относительно
), совпадает с классом частичных функций, частично рекурсивных относительно 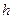 (соответственно относительно системы
(соответственно относительно системы 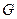 ).
).
Из тезиса Тьюринга вытекает тезис Чёрча.
 2015-03-27
2015-03-27 9168
9168








