2.1. Использование функции fminsearch
Вызывая справочную функцию help, изучить параметры и способы использования функции fminsearch. Пояснения поместить в отчёт.
2.2. Задача: найти минимум целевой функции
y=fun2(x)=3|x1|+|x2|.
Решение получаем с помощью следующего оператора:
>> [x,f]=fminsearch ('3*abs(x(1))+abs(x(2))',[1;1])
Результат прокомментировать
x = 1.0e-004 *
-0.1439
0.3565
f = 7.8809e-005
2.3. Создать m-файл, содержащий следующую функцию:
function z=discont(x)
if (x(1)> 0) & (x(2) >= 0) % 1
z = x(1)+2*x(2);
elseif (x(1)<= 0) & (x(2) >= 0) % 2
z = -2*x(1)+x(2);
elseif (x(1)< 0) & (x(2) <= 0) % 3
z = -x(1)-2*x(2);
elseif (x(1)>= 0) & (x(2) < 0) % 4
z = 2*x(1)-x(2);
elseif (x(1)== 0) & (x(2) == 0) % 00
z = 0;
end
Задать режим работы функции fminsearch:
>> options=optimset ('Display','off');
Задать начальную точку поиска:
>> x0=[0.5; 0.1];
Вызвать функцию поиска:
>> [x,f,e_flag] = fminsearch (@discont,x0,options)
Результаты прокомментировать.
x = 1.0e-003 *
0.0640
-0.1342
f = 2.6229e-004
e_flag = 1
Проведите расчёт, изменив значение x0.
Результаты выполненного пункта прокомментировать.
2.4. Поиск минимума «банана Розенброка»
Функция Розенброка имеет вид:
z=100(x2–x12)2 +(1–x1)2
Создайте m-файл функции:
function f=Rosenbrock(x)
f = 5*(x(2)-x(1)^2)^2+(1-x(1))^2;
Для вычислений используйте функцию следующего m-файла:
function prog15_5
X0=-3:0.1:3;
Y0=-2:0.1:5;
[X Y]=meshgrid(X0,Y0);
s=size(X); Z=zeros(s);
for i=1:s(1)
for j=1:s(2)
Z(i,j) = Rosenbrock([X(i,j); Y(i,j)]);
end
end
axes('Xlim',[-3 3], 'Ylim',[-2 5]);
axis equal; grid off; hold on;
v=1:2:10; V=10:4:20;
contour(X,Y,Z,[v V]);
xlabel('x1'); ylabel('x2');
x0=[-2; 2];
line(x0(1),x0(2), 'Marker', '.', 'MarkerSize', 10);
[x,f]=fminsearch('5*(x(2)-x(1)^2)^2+(1-x(1))^2', x0)
line(x(1),x(2), 'Marker', '.', 'MarkerSize', 20);
plot([x0(1),x(1)], [x0(2),x(2)],'k-')
После расчёта по команде
>> prog15_5
прокомментируйте результат.
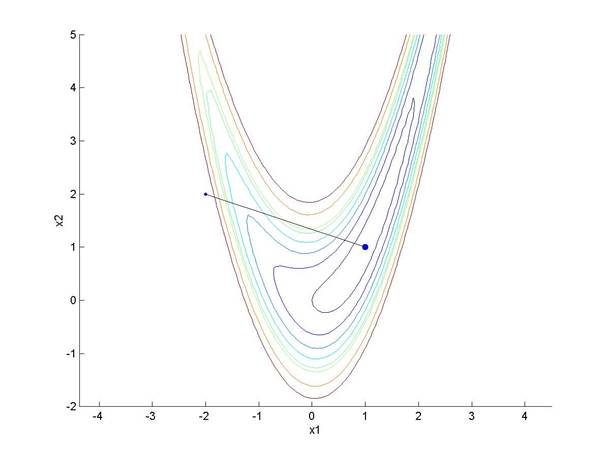
x =
1.0000
1.0000
f = 1.8161e-009
2.5. Если выполнить следующее обращение к функции, она выведет дополнительные параметры – признак завершения работы и информацию о числе шагов поиска и обращений к вычислению целевой функции, а также название алгоритма поиска:
>> x0=[-2; 2];
>> [x,f,e_flag,inform]=fminsearch('5*(x(2)-x(1)^2)^2+(1-x(1))^2', x0)
x =
1.0000
1.0000
f = 1.8161e-009
e_flag = 1
inform =
iterations: 61
funcCount: 115
algorithm: 'Nelder-Mead simplex direct search'
2.6. С помощью функции fminsearch найти минимум следующих функций нескольких переменных:
Таблица 2.
| Вариант | Вид функции fun(x, у) | Начальные точки поиска |
| 1(1, 9, 17) | x2 – xy + y2 – 2x + y | [0; 1] |
| 2(2, 10, 18) | x2 y3 (6 – x – y) | [1; 1] |
| 3(3, 11, 19) | x3 + y3 – 3xy | [0; 0] |
| 4(4, 12, 20) | x4 + y4 – x2 – 2xy – y2 | [0; 0] |
| 5(5, 13, 21) | 2x4 + y4 – x2 – 2y2 | [1; 0.5], [–1, –2] |
| 6(6, 14, 22) | xy + 50/x + 50/y | [2; 1] |
| 7(7, 15, 2) | xy (1 – x2– y2)1/2 | [0.5; –0.5], [–0.5; 0.5] |
| 8(8, 16, 21) | (x2 + y2)1/2 – 1 | [1; 1] |
| 9(9, 18, 3) | x2 + xy + y2 – 4 ln x – 10 ln y | [2; 1] |
| 10(10, 19, 1) | (x – y + 1)2 | [2; 2] |
| 11(11, 20, 2) | xy ln (x2 + y2) | [1; 1], [–1; –1] |
| 12(12, 21, 3) | x + y + 4 sin x sin y | [0; 0], [3; 3] |
| 13(13, 22, 4) | x2 + y2 + z2 + 2x + 4y – 6z | [0; –1; 2] |
| 14(14, 20, 5) | x2 + y2 + z2 + 12xy + 2z | [0; –10; 0] |
| 15(15, 21, 6) | x + y2/4x + z2/y + 2/z | [0; 0; 0] |
| 16(16, 3, 7) | xy2z3 (7 – x – 2y – 3z) | [0; 0; 0] |
| 17(17, 10, 4) | e2x+3y (8 x2 – 6xy + 3y2) | [1; 2] |
| 18(18, 11, 5) | exp{x2 – y}(5 – 2x + y) | [–1; –1] |
| 19(19, 12, 6) | sin x + cos y + cos (x – y) | [2; 2] |
| 20(20, 13, 9) | sin x sin y sin (x + y) | [1; 1] |
| 21(21, 14, 8) | (x2 + y2) exp{–(x2 + y2)} | [1; 1] |
| 22(22, 15, 10) | sin x + sin y + sin z – sin(x+y+z) | [1; 1; 1] |
В отчёте представьте результаты с комментариями.
3. Использование функции fminunc
Для ускорения поиска в функцию необходимо включить формулы для вычисления градиента и гессиана. Это необходимо указать в списке управляющих параметров для функции минимизации:
Options=optimset('Display', 'final','GradObj', 'on', 'Hessian', 'on');
[x,f1,e_flag,out,grad,hes]=fminunc(@Descartes,x0,options)
В режиме функции help изучить параметры и способы использования функции fminunc. Записать пояснения в отчёт.
3.1. Текст следующей функции записать в соответствующий m-файл:
function prog15_6
axes('Xlim',[-1.5 2.5], 'Ylim',[-1.5 2.5]);
axis equal; grid off; hold on;
xlabel('x1'); ylabel('x2');
colormap copper;
X0=-1.5:0.05:2.5;
[X Y]=meshgrid(X0);
s=size(X); Z=zeros(s);
for i=1:s(1)
for j=1:s(2)
Z(i,j) = Descartes([X(i,j); Y(i,j)]);
end
end
V=-0.8:0.2:1;
contour(X,Y,Z,V);
options=optimset('Display', 'final','GradObj', 'on', 'Hessian', 'on');
x0=[-2; 2];
line(x0(1),x0(2), 'Marker', '.', 'MarkerSize', 10);
[x,f1,e_flag,out,grad,hes]=fminunc(@Descartes,x0,options)
line(x(1),x(2), 'Marker', '.', 'MarkerSize', 20);
plot([x0(1),x(1)], [x0(2),x(2)],'k-')
function [f,g,H] = Descartes(x)
f = x(1)^3+x(2)^3-3*x(1)*x(2);
if nargout > 1
g = [3*(x(1)^2-x(2)); 3*(x(2)^2-x(1))];
end
if nargout > 2
H = [6*(x(1) -3; -3 6*x(2)];
end
end
Внимательно изучите текст программы, в отчёте кратко опишите алгоритм её работы.
Вызов функции имеет вид:
>> prog15_6
Результат её выполнения:
Optimization terminated successfully:
Relative function value changing by less than OPTIONS.TolFun
x =
1.0000
1.0000
f1 = -1
e_flag = 1
out =
iterations: 6
funcCount: 6
cgiterations: 5
firstorderopt: 6.9849e-010
algorithm: [1x32 char]
grad = 1.0e-009 *
0.6985
0.6985
hes =
6.0000 -3.0000
-3.0000 6.0000
Поясните полученный результат.
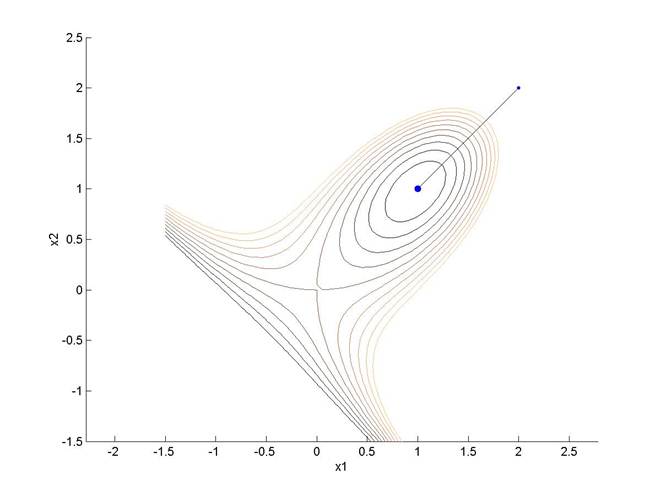
Декартов лист.
3.2. Задание: По образцу рассмотренного примера применить функцию fminunc к минимизации функций предыдущего пункта с использованием градиента и гессиана. Выражения первых и вторых производных привести в отчёте. Сравнить полученные результаты.
3.3. Задача об управлении роботом
Вычисление координат схвата:
function x=coord(q,l)
Q=cumsum(q);
x=[sum(l.*cos(Q)); sum(l.*sin(Q))];
Целевая функция:
function d=dist(q,l,xc)
x=coord(q,l);
d=norm(x-xc);
Исходные данные:
q0=[0.7 -1 0.5];
l=[5 5 5];
xc=[12; 0];
Обращение к функции минимизации:
[q,f]=fminunc(@dist,q0,[],l,xc)
Результат расчёта:
Optimization terminated successfully:
Search direction less than 2*options.TolX
q = 0.8650 -1.5768 0.6036
f = 3.0602e-007
Графическая иллюстрация получается с помощью программы:
function prog15_7
axes('Xlim',[-1 15], 'Ylim',[-1 10]);
axis equal; grid on; hold on;
l=[5 5 5];
xc=[12; 0];
qInit=[0.7 -1 0.5];
[XInit,YInit]=hinges(qInit,l);
plot(XInit, YInit,'k:');
qOptim=[0.8650 -1.5768 0.6036];
[XOptim,YOptim]=hinges(qOptim,l);
plot(XOptim, YOptim,'k-','LineWidt',2);
plot([0],[-0.3],'k^','MarkerSize',15);
plot(XInit(1:3), YInit(1:3),'ko');
plot([XInit(4)], [YInit(4)],'ks', 'MarkerSize', 15);
plot(XOptim(1:3), YOptim(1:3),'ko');
plot([XOptim(4)], [YOptim(4)],'ks', 'MarkerSize', 15);
xlabel('x1'); ylabel('x2');
legend('Начальное','Конечное');
title('Два положения манипулятора');
function [X,Y] = hinges(q,l)
Q=cumsum(q);
x=l.*cos(Q); y=l.*sin(Q);
x=[0 x]; y=[0 y];
X=cumsum(x); Y=cumsum(y);
Вызов:
>> prog15_7
Результат:
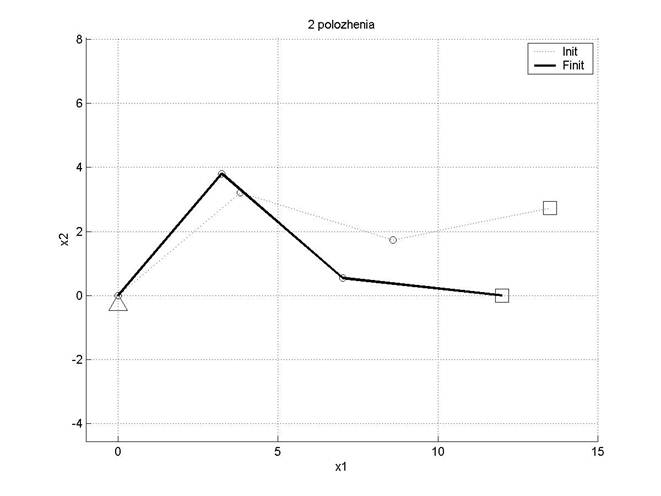
Сделать пояснения к рисунку.
Изменить целевую точку схвата:
xc=[10; 5];
Получить соответствующие значения обобщённых координат робота, а также дополнительную информацию о ходе вычислений.


 2015-03-27
2015-03-27 778
778







