Известны следующие параметры механизма (рис. 2.1): 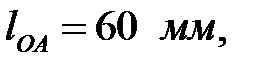
 ,
, 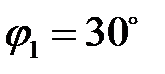 ,
, 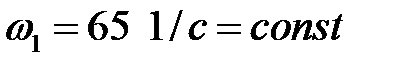 . Направление вращения кривошипа – против часовой стрелки
. Направление вращения кривошипа – против часовой стрелки
Требуется определить линейные скорости и ускорения точек механизма, а также угловые скорости и ускорения звеньев.
2.1.1 Построение плана положений механизма
Выражаем все длины звеньев в метрах:
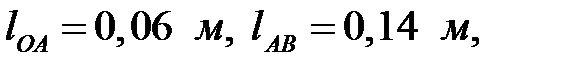
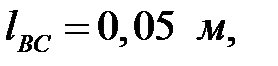
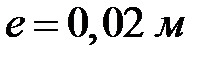 .
.
Определяем масштабный коэффициент длин, представляющий собой отношение действительной длины в метрах к длине отрезка на чертеже в миллиметрах. Изображаем длину кривошипа 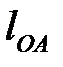 на чертеже отрезком
на чертеже отрезком 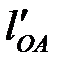 , равным, например, 30 мм. Тогда масштабный коэффициент будет иметь величину
, равным, например, 30 мм. Тогда масштабный коэффициент будет иметь величину
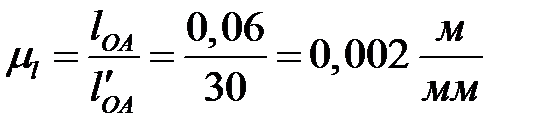 .
.
Остальные длины звеньев, изображенные на чертеже, будут иметь следующие значения:
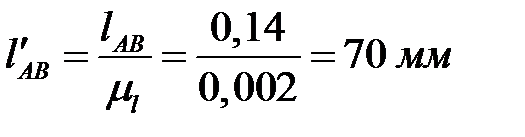 ,
, 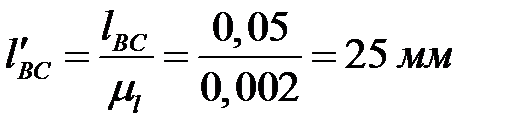 ,
, 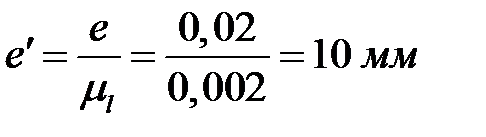 .
.
Из произвольной точки О под углом 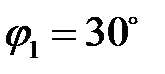 откладываем отрезок
откладываем отрезок 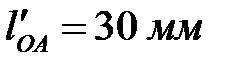 . Далее проводим горизонтальную прямую Х, отстоящую от точки О по вертикали на величину
. Далее проводим горизонтальную прямую Х, отстоящую от точки О по вертикали на величину  . Из точки
. Из точки  раствором циркуля, равным
раствором циркуля, равным  , на оси Х делаем засечку, получая точку
, на оси Х делаем засечку, получая точку 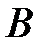 . На продолжении линии АВ откладываем расстояние
. На продолжении линии АВ откладываем расстояние 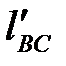 и отмечаем точку С. Указываем положение центров масс
и отмечаем точку С. Указываем положение центров масс 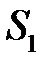 ,
, 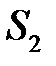 ,
, 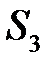 , которые находятся в серединах отрезков
, которые находятся в серединах отрезков 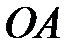 ,
, 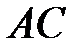 и в точке
и в точке 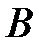 . Аналогичным образом можно построить и другие положения механизма, которые отличаются величинами угла
. Аналогичным образом можно построить и другие положения механизма, которые отличаются величинами угла 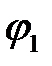 .
.
2.1.2 Построение плана скоростей
Определяем скорость точки А
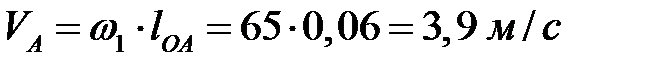 .
.
Находим масштабный коэффициент скоростей, для чего полученную величину делим на длину вектора этой скорости, выбранную равной 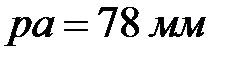
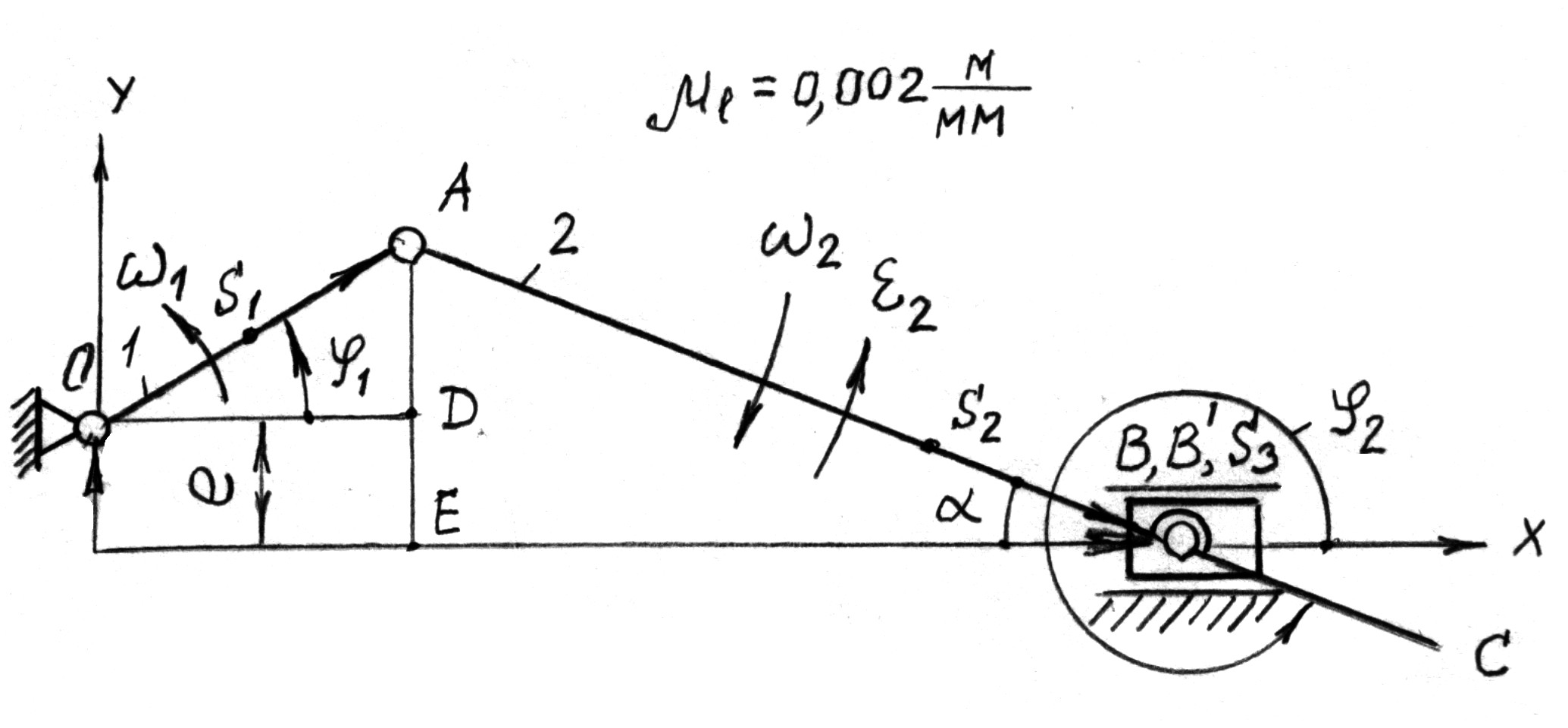
Рисунок 2.1
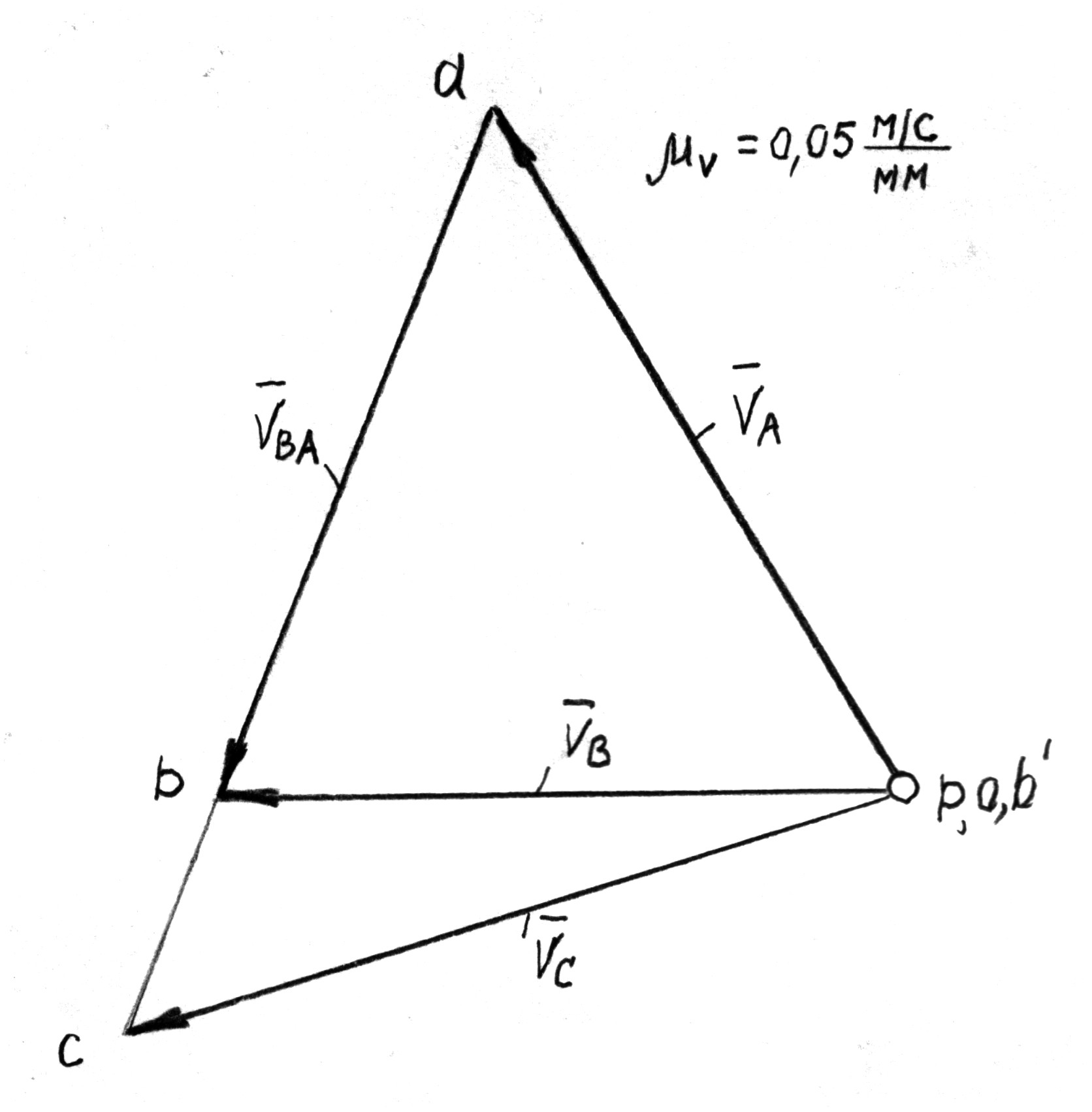
Рисунок 2.2
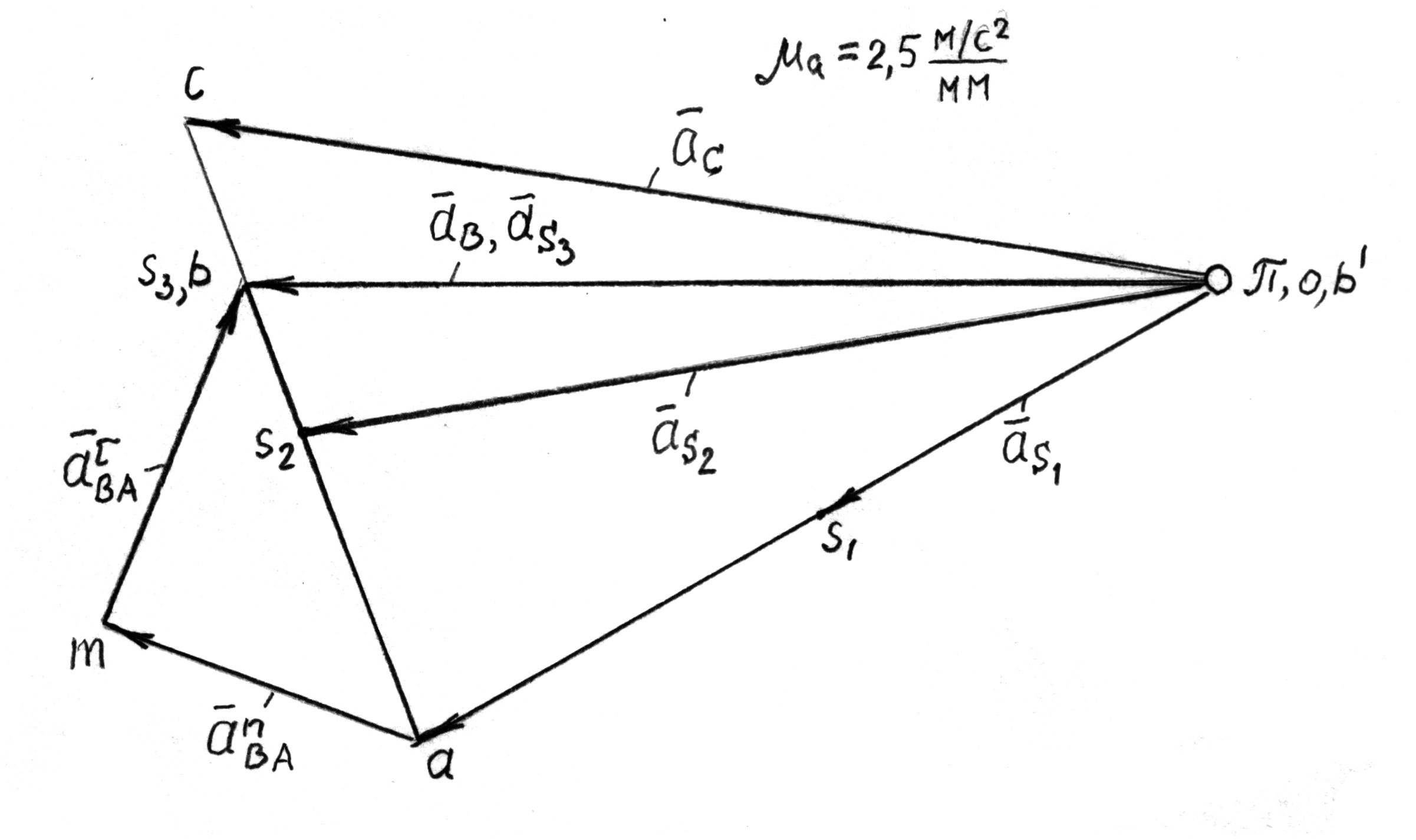
Рисунок 2.3
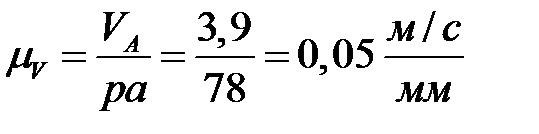 .
.
Из произвольной точки  (полюса скоростей) проводим вектор
(полюса скоростей) проводим вектор 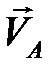 (рис. 2.2) длиной 78 мм, который перпендикулярен кривошипу ОА и направлен в сторону его вращения. Скорость точки В находим графически, используя векторные уравнения
(рис. 2.2) длиной 78 мм, который перпендикулярен кривошипу ОА и направлен в сторону его вращения. Скорость точки В находим графически, используя векторные уравнения
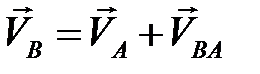 ,
, 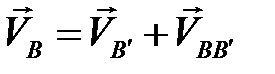 .
.
Здесь точка 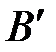 , принадлежит стойке Х.
, принадлежит стойке Х.
Так как скорости точек  и
и 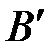 равны нулю, то точки
равны нулю, то точки 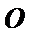 и
и 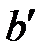 помещаем в полюсе. Уравнения решаются так. Из точки
помещаем в полюсе. Уравнения решаются так. Из точки 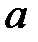 проводим линию, перпендикулярную шатуну АВ, а из полюса – прямую, параллельную стойке Х. На пересечении ставим стрелки, получая векторы скоростей
проводим линию, перпендикулярную шатуну АВ, а из полюса – прямую, параллельную стойке Х. На пересечении ставим стрелки, получая векторы скоростей 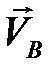 и
и 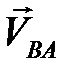 . Для нахождения положения точки
. Для нахождения положения точки 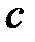 используем отношение
используем отношение
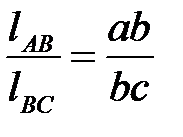 ,
, 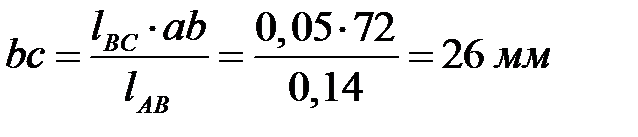 .
.
Откладываем эту величину на продолжении линии 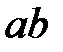 . Полученную точку соединяем с полюсом, получая вектор скорости
. Полученную точку соединяем с полюсом, получая вектор скорости 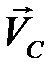 . Численные значения скоростей получаем путем замера каждого вектора и умножения полученной величины на
. Численные значения скоростей получаем путем замера каждого вектора и умножения полученной величины на 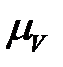
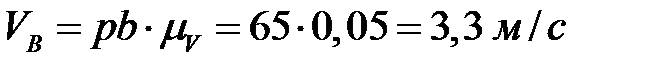 ,
, 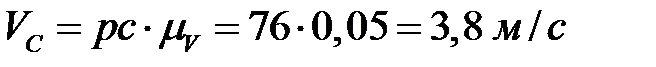 ,
,
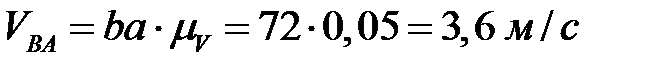 .
.
Находим угловую скорость 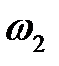 шатуна
шатуна
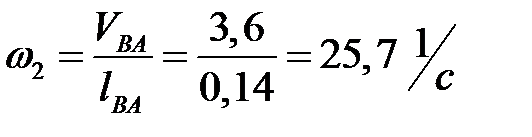 .
.
Направление этой скорости можно найти, поместив вектор 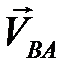 в точку В и посмотрев, куда повернется шатун АВ относительно точки А. В данном случае – по часовой стрелке. Циркулем обозначим дуговую стрелку скорости
в точку В и посмотрев, куда повернется шатун АВ относительно точки А. В данном случае – по часовой стрелке. Циркулем обозначим дуговую стрелку скорости 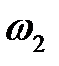 , ставя ножку циркуля в точку А.
, ставя ножку циркуля в точку А.
Угловая скорость 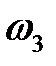 ползуна равна нулю.
ползуна равна нулю.
2.1.3 Построение плана ускорений
Ускорение точки А в общем случае складывается из двух составляющих: 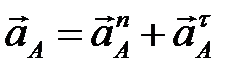 .
.
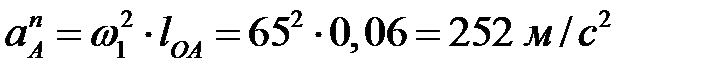
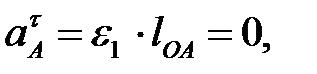 т.к.
т.к. 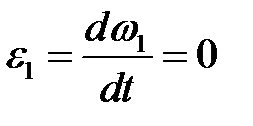 .
.
Следовательно, 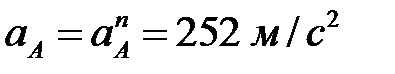 .
.
Масштабный коэффициент ускорений можно найти путем деления этой величины на длину  вектора
вектора 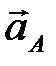 на чертеже, равную, например, 101мм
на чертеже, равную, например, 101мм
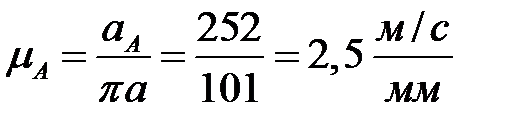 .
.
Ускорение точки А направлено параллельно кривошипу ОА от точки А к центру О. Из произвольной точки  (полюса ускорений) (рис. 2.3) проводим вектор
(полюса ускорений) (рис. 2.3) проводим вектор 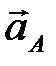 длиной 101 мм. Ускорение точки В находим графо-аналитически, решая систему векторных уравнений
длиной 101 мм. Ускорение точки В находим графо-аналитически, решая систему векторных уравнений
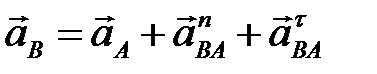 ,
, 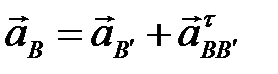 .
.
Ускорения 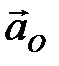 и
и 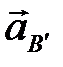 равны нулю, поэтому точки
равны нулю, поэтому точки 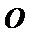 и
и 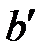 помещаем в полюсе.
помещаем в полюсе.
Определяем ускорение 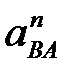
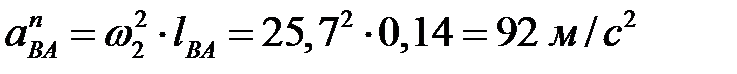 .
.
Это ускорение направлено параллельно шатуну ВА от точки В к точке А. Длина вектора этого ускорения
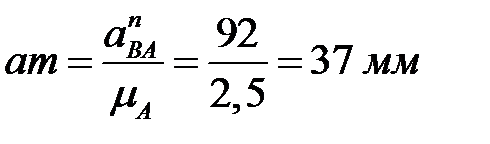 .
.
Следует отметить, что если длина какого-то вектора оказывается меньшей 3 мм, то вместо него на плане ускорений ставится точка, около которой указывается обозначение этого ускорения.
В конце вектора 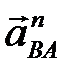 проводим прямую, перпендикулярную шатуну АВ. Из полюса
проводим прямую, перпендикулярную шатуну АВ. Из полюса 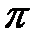 направляем луч, параллельный стойке Х. На пересечении ставим стрелки, получая векторы
направляем луч, параллельный стойке Х. На пересечении ставим стрелки, получая векторы 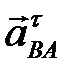 и
и 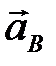 . Точки
. Точки  и
и 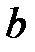 соединяем и на продолжении от точки
соединяем и на продолжении от точки 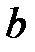 откладываем отрезок
откладываем отрезок 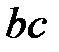 , получаемый из соотношения
, получаемый из соотношения
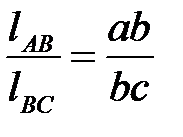 ,
, 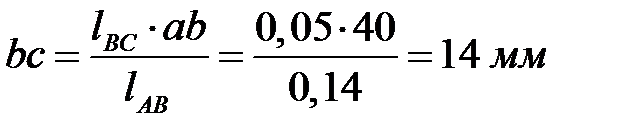 .
.
Точку 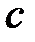 соединяем с полюсом, получая вектор
соединяем с полюсом, получая вектор 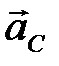 В серединах отрезков
В серединах отрезков 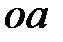 и
и 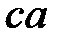 находим положения точек
находим положения точек 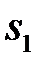 и
и 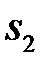 , соединяя которые с полюсом, находим векторы ускорений
, соединяя которые с полюсом, находим векторы ускорений 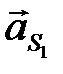 и
и 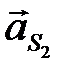 . Вектор ускорения
. Вектор ускорения 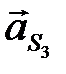 совпадает с вектором
совпадает с вектором 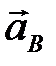 .
.
Замеряя длины векторов неизвестных ускорений, находим их численные значения
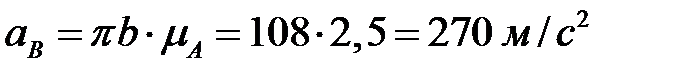 ,
,
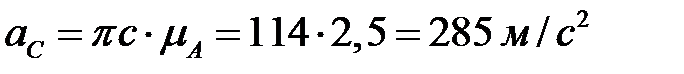 ,
,
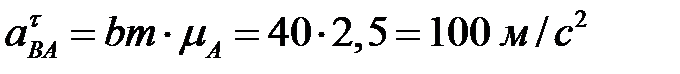 ,
,
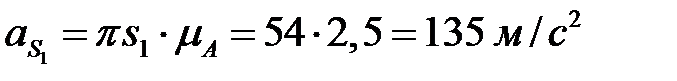 ,
,
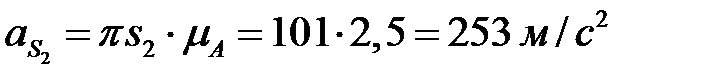 ,
,
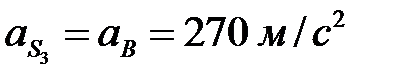 .
.
Определяем угловое ускорение 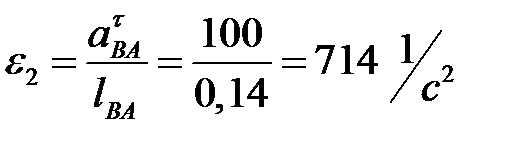 .
.
Переносим вектор 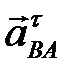 в точку В механизма и находим, что угловое ускорение направлено против часовой стрелки. Угловое ускорение
в точку В механизма и находим, что угловое ускорение направлено против часовой стрелки. Угловое ускорение 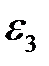 ползуна равно нулю.
ползуна равно нулю.
 2015-03-07
2015-03-07 6702
6702
