Пусть 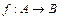 . Тогда функция является:
. Тогда функция является:
Инъективной, или инъекцией, если 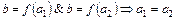 .
.
Сюръективной, или сюръекцией, если 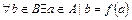 .
.
Биективной, или биекцией, если она инъективная и сюръективная.
Замечание.
Биективную функцию также называют взаимно однозначной.
Рис.5.1. иллюстрирует понятия отношения, функции, инъекции, сюръекции и биекции.
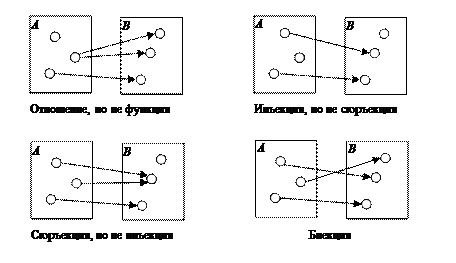

Рисунок 5.1.
Теорема.
Если 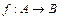 – тотальная биекция (
– тотальная биекция (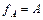 ), то отношение
), то отношение 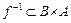 (обратная функция) является биекцией.
(обратная функция) является биекцией.
Доказательство.
Поскольку 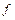 – биекция, имеем
– биекция, имеем 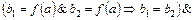
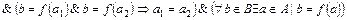 .
.
Покажем, что 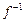 – функция.
– функция.
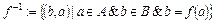
Поскольку 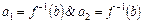 .
.
Тогда 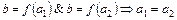 .
.
Покажем, что 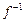 – инъекция. Пусть
– инъекция. Пусть 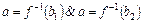 .
.
Тогда 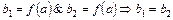 . Покажем от противного, что
. Покажем от противного, что 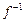 – сюръекция.
– сюръекция.
Пусть 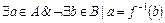 . Тогда
. Тогда 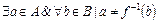 . Обозначим этот элемент
. Обозначим этот элемент 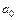 . Имеем:
. Имеем: 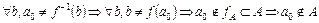 .
.
 2015-03-08
2015-03-08 7818
7818








