2015-03-08
2273
Понятие “функции” является одним из основополагающих в математике, в данном случае подразумевается прежде всего функции, отображающие одно конечное множество объектов в другое конечное множество, мы избегаем использование термина “отображение” и предпочитаем слово “функция” в расчете на постоянное сопоставление читателем математического понятия функции с понятием функции в языках программирования.
Определения 5.1. Говорят, что между множествами А и В определено соответствие Г, если задано некоторое произвольное подмножество декартового произведения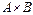 
.
Определения 5.2. Отображением множества А на множество В называется такое соответствие, которое каждому элементу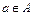 
сопоставляется по крайней мере один элемент 
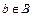. Тогда элемент b называется образом элемента а, a a – прообразом элемента b, или переменной, или аргументом.
Определения 5.3. Соответствие, при котором каждому а Î А сопоставляется один и только один элемент b Î B,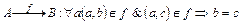 
, называется функциональным соответствием, или функцией из А в В, и обозначается следующим образом 
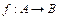или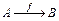 
.
Если b=f(a), то а называют аргументом, а b – значением функции.
Замечание.
Вообще всякому отношению R из A в В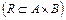 
можно сопоставить (тотальную) функцию 
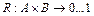(эта функция называется характеристической функцией отношения), полагая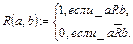 
Пусть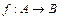 
, тогда
Область определения функции: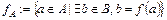 
.
Область значения функции: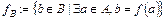 
.
Определения 5.4. Если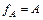 
,то функция называется тотальной, а если 
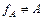, то – частичной.
Определения 5.5. Суждением функции 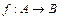на множестве 
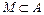называется функция 
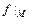, определяемая следующим образом: 
.
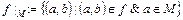Для тотальной функции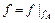 
.
Определения 5.6. Функция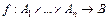 
называется функцией n аргументов, или n-местной функцией.
