Теоретические сведения. Построение минимального покрывающего дерева

Построение минимального покрывающего дерева

ЦЕЛЬ РАБОТЫ

11.1.1 Ознакомиться с теоретическими сведениями.

11.1.2 Получить практические навыки по построению минимальных покрывающих деревьев.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

11.2.1 Методические указания по выполнению практической работы.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

11.3.1 Изучить методические указания к практической работе.

11.3.2 Постройте минимальное покрывающее дерево в соответствии со своим вариантом.

СОДЕРЖАНИЕ ОТЧЕТА

11.4.1 Цель работы

11.4.2 Методические рекомендации

11.4.3 Порядок выполнения работы

11.4.4 Ответы на контрольные вопросы

11.4.5 Выводы

КОНТРОЛЬНЫЕ ВОПРОСЫ

11.5.1 Что такое дерево?

11.5.2 Что называется ветвью?

11.5.3 Что такое лист?

11.5.4 Что такое лес?

11.5.5 Что такое остов?

11.5.6 Что такое минимальное покрывающее дерево?

11.5.7 В чем суть алгоритма Крускала?

11.5.8 В чем суть алгоритма Борувки?

ПРИЛОЖЕНИЕ 1

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Остовом связного графа называется любой его подграф, содержащий все вершины графа и являющийся деревом.

Постановка задачи

Итак, имеется n городов, которые нужно объединить в единую телефонную сеть. Для этого достаточно проложить (n-1) телефонных линий между городами. Как соединить города так, чтобы суммарная стоимость соединений (телефонного кабеля) была минимальна?

В общем случае, задачу можно сформулировать так. Пусть дан связный, неориентированный граф с весами на ребрах G(V, E), в котором V — множество вершин (контактов), а E — множество их возможных попарных соединений (ребер). Пусть для каждого ребра (u,v) однозначно определено некоторое вещественное число w(u,v) — его вес (длина или стоимость соединения). w() называется весовой функцией. Задача состоит в нахождении такого связного ациклического подграфа T ⊂ G, содержащего все вершины, что суммарный вес его ребер будет минимален.

Так как T связен и не содержит циклов, он является деревом и называется остовным или покрывающим деревом. Остовное дерево T, у которого суммарный вес его ребер минимален, называется минимальным остовным или минимальным покрывающим деревом

Алгоритм Борувки

Схема работы алгоритма представлена на рисунках Б1-Б5.

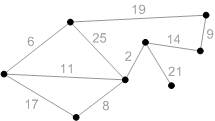Рис. Б1. Начальная фаза. Минимальный покрывающий лес состоит из всех вершин графа и пустого множества ребер.

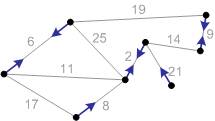
Рис. Б2. Для каждой компоненты связности (для каждой вершины) находим безопасные ребра. Они отмечены стрелками от компоненты вдоль безопасного ребра.

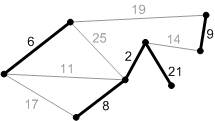
Рис. Б3. Добавляем безопасные ребра к минимальному остовному лесу.

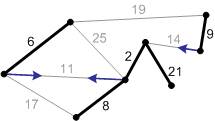
Рис. Б4. Находим безопасные ребра для каждой компоненты связности.

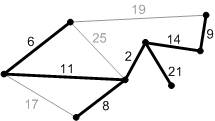
Рис. Б5. Добавляем найденные ребра. Минимальное остовное дерево построено.

Алгоритм Крускала

Алгоритм Крускала объединяет вершины графа в несколько связных компонент, каждая из которых является деревом. На каждом шаге из всех ребер, соединяющих вершины из различных компонент связности, выбирается ребро с наименьшим весом. Необходимо проверить, что оно является безопасным. Безопасность ребра гарантируется ранее доказанной теоремой о безопасных ребрах. Так как ребро является самым легким из всех ребер, выходящих из данной компоненты, оно будет безопасным.

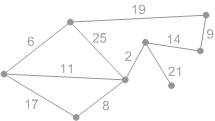
Рис. К1. Начальная фаза. Минимальный покрывающий лес пуст.

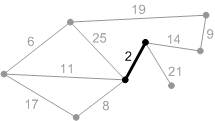
Рис. К2. Перебираем ребра в порядке возрастания веса: первое ребро с весом 2. Добавляем его к А.

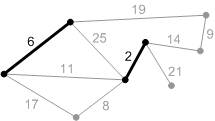
Рис. К3. Следующее безопасное ребро с весом 6. Добавляем его.

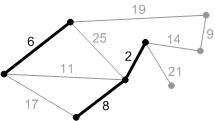
Рис. К4.

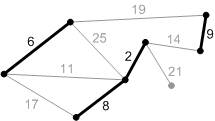Рис. К5.

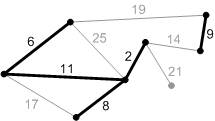Рис. К6.

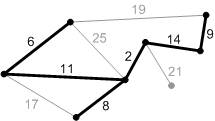Рис. К7.

Рис. К8. Ребра с весом 17, 19 и 25 – не безопасные. Их концы лежат в одной компоненте связности. Ребро с весом 21 – безопасное, поэтому добавляем его. Минимальное остовное дерево построено

ПРИЛОЖЕНИЕ 2