1) Во всех точках, лежащих внутри интервала сходимости, сумма степенного ряда является непрерывной функцией переменной x:
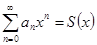
2) Степенной ряд можно почленно интегрировать внутри интервала сходимости:
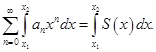
3) Внутри интервала сходимости степенной ряд можно почленно дифференцировать:
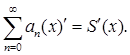
При почленном интегрировании и дифференцировании степенных рядов их интервалы сходимости не меняются.
Пример 4. Найти сумму ряда
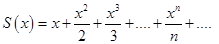 (3.6)
(3.6)
Решение. Найдем сначала интервал сходимости этого ряда n
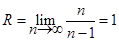
Следовательно, интервал сходимости ряда (-1, +1). Продифференцировав (3.6), имеем
S¢(x) = 1 + x + x2 +... + xn +....
Правая часть этого выражения - геометрический ряд с q = x, который сходится при ½x½<1. Поэтому, используя формулу суммы сходящейся геометрической прогрессии, получим
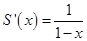
Отсюда сумму исходного ряда найдем интегрированием
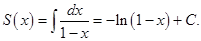
Найдем C. Из (5.6) следует, что S(0) = 0. Следовательно,
0 = - ln (1-0) + C, C = 0.
Таким образом, S(x) = - ln (1-x) = 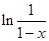
 .
.
Наряду со степенными рядами относительно переменной х часто рассматривают степенные ряды по переменной (x-a), т.е. ряды вида
C0 + C1(x-a) + C2(x-a)2 +... Cn (x-a)n +... (3.7)
Очевидно, что этот ряд подстановкой y = (x - a) превращается в ряд типа (3.3). Поэтому, если степенной ряд (3.3) имеет интервал сходимости - R < x < R, то соответствующий ряд вида (3.7) имеет интервал сходимости (a - R) < x < (a + R), центр которого расположен в точке x = a.
Ряд Тейлора. Пусть функция f(x) в точке х = а имеет производные любого порядка. Предположим, что имеется сходящийся степенной ряд
а0 + а1(x-a) + а2(x-a)2 +...+ аn (x-a)n +... = 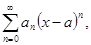 (3.8)
(3.8)
сумма которого равна функции f(x), т.е.
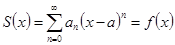 (3.9)
(3.9)
Найдем коэффициенты такого ряда. Очевидно, что f(a) = а0. Продифференцировав (3.8) в точке х=а, имеем а1=f¢(a). Продифференцировав (3.8) в точке х=а дважды, получим а2 = (f¢¢(a))/2. Продолжая дифференцирование равенства (3.8) можно убедится, что коэффициенты ряда (находятся по формуле
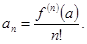
Степенной ряд вида
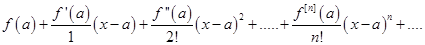
называется рядом Тейлора для функции f(x).
В частном случае при a= 0 ряд Тейлора имеет вид
f(x) = 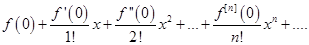 (3.10)
(3.10)
и его называют рядом Маклорена.
Пример 5. Разложить в ряд Тейлора функцию f(x) = ex.
Решение. Поскольку ex =(ex)¢=(ex)¢¢ =...(ex)n, то при x=0 для f(x)= ex имеем
f(0) = 1; f¢(0) = 1; f¢¢(0) = 1;...; f(n)(0) = 1;....
Следовательно, ряд Маклорена функции y = ex имеет вид
ex = 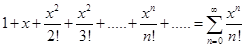 (3.11)
(3.11)
Ряд (3.11) сходится на всей числовой оси к функции y=ex.
Пример 6. Разложить в ряд маклорена функцию f(x) = sinx.
Решение. Для функции f(x) = sin x имеем:
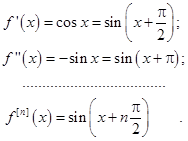
Следовательно, ряд Маклорена для sin x:
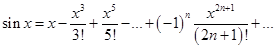
или
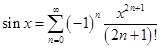
Аналогично получается разложение для функции cos x:
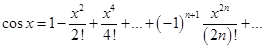
или
cosx= 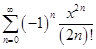 .
.
Подобным образом можно получить разложения в ряд Тейлора или Маклоренаи многих других функций.
 2015-03-07
2015-03-07 8667
8667
