Самыми простыми среди задач ИСО являются так называемые задачи линейного программирования. Для них характерно:
· целевая функция W линейно зависит от элементов решения х1, х2,..., хn
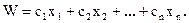
· ограничения, налагаемые на элементы решения, имеют вид линейных равенств или неравенств относительно элементов решения.
Такие задачи довольно часто встречаются на практике, например, при решении проблем, связанных с распределением ресурсов, планированием производства, организацией работы транспорта и т. д.
Для примера, задача о пищевом рационе.
Ферма производит откорм скота. Для простоты допустим, что имеется всего четыре вида продуктов: П1, П2, П3, П4; стоимость единицы каждого продукта равна соответственно с1, с2, с3, с4. Из этих продуктов требуется составить пищевой рацион, который должен содержать: белков - не менее b1 единиц; углеводов — не менее b2 единиц; жиров — не менее b3 единиц.
Таблица 2.
| Про- | Элементы | ||
| дукты | белки | углеводы | жиры |
| П1 | а11 | а12 | а13 |
| П2 | а21 | а22 | а23 |
| П3 | а31 | а32 | а33 |
| П4 | а41 | а42 | а43 |
Для продуктов П1, П2, П3, П4 содержание белков, углеводов и жиров aij(в единицах на единицу продукта) известно и задано в таблице.
Требуется составить такой пищевой рацион (т. е. назначить количества продуктов П1, П2, П3, П4, входящих в него), чтобы условия по белкам, углеводам и жирам были выполнены и при этом стоимость рациона была минимальна.
Составим математическую модель. Обозначим х1, х2, х3, х4 количества продуктов П1, П2, П3, П4, входящих в рацион. Целевую функцию требуется минимизировать. Она линейно зависит от элементов решения.
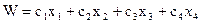 , или
, или
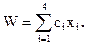
Итак, вид целевой функции известен и она линейна. Запишем теперь в виде формул ограничительные условия по белкам, углеводам и жирам. Учитывая, что в одной единице различных продуктов содержится различное количество ингредиентов aij, получим три неравенства.
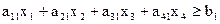
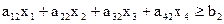
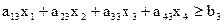
Эти линейные неравенства представляют собой ограничения, накладываемые на элементы решения х1, х2, х3, х4.
Таким образом, поставленная задача сводится к следующей: найти такие неотрицательные значения переменных х1, х2, х3, х4, чтобы они удовлетворяли ограничениям — неравенствам и одновременно обращали в минимум линейную функцию этих переменных:
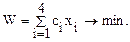
Это и есть математическая модель нашей задачи о рационе.
Классически, такие задачи решают симплексным методом.
Графическое решения задачи линейного программирования. Кооператив выпускает два вида продукции – стекло и пенопласт. Трудозатраты на производство стекла – 20ч., пенопласта – 10ч. В кооперативе работают 10 рабочих по 40 ч. в неделю. Оборудование позволяет производить не более 15 т стекла и 30 т пенопласта в неделю. Прибыль от реализации 1 т стекла – 50 руб.; 1т пенопласта – 40 руб. Сколько материалов необходимо выпустить для получения максимальной прибыли?
Математическая модель представляется следующей системой уравнений:
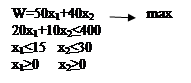 |
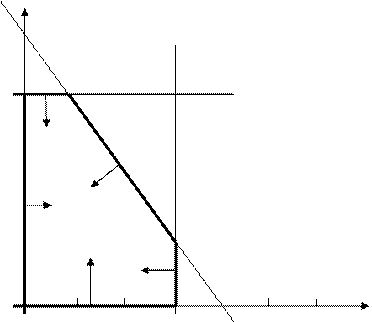
На рисунке показано область допустимых решений рассматриваемой задачи. Она представляет собой совокупность точек, удовлетворяющих каждому ограничению.
 |
х2
5 х1
5 10 15 20 25
Рис.9. Множество допустимых решений.
Если решение существует и единственное, то оно лежит в вершине области допустимых значений (без доказательства). Что бы получить оптимальное решение задачи, необходимо осуществить перебор вершин и выбрать ту, в которой целевая функция принимает максимальное значение.
Это положение лежит в основе симплекс-метода, позволяющего получить численное решение задачи линейного программирования.
В нашем примере оптимальным решением является вершина с координатами (5;30). W(5,30)=1450.
Оптимальное решение может быть не единственным. Тогда все точки какой либо прямой, ограничивающей область решений, соответствуют оптимальному решению.
 2015-03-08
2015-03-08 714
714








