В данном разделе готовим расчётные выражения, необходимые для расчёта магнитной цепи (табл. 3).
Таблица 3
| Параметр | Е * и Ф* | ||||
| 0,5 | 1,1 | 1,2 | 1,3 | ||
| Е, В | 66,5 | ||||
| Ф=3,21∙10-4 Е, Вб | 0,0213 | 0,0427 | 0,0469 | 0,0514 | 0,0555 |
| В δ=6,18∙10-3 Е, Тл | 0,411 | 0,822 | 0,902 | 0,989 | 1,07 |
| F δ=22 Е, А | |||||
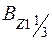 = 10,8∙10-3 Е, Тл = 10,8∙10-3 Е, Тл
| 0,718 | 1,44 | 1,58 | 1,73 | 1,87 |
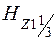 , А/м , А/м
| |||||
FZ1 =6,68∙10-2 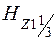 , А , А
| 13,4 | ||||
| Ва =9,9∙10-3 Е, Тл | 0,66 | 1,32 | 1,45 | 1,58 | 1,71 |
| ξ | 0,62 | 0,38 | 0,33 | 0,31 | 0,27 |
| На, А/м | |||||
| Fa =14,7∙10-2ξ На, А | 15,7 | 67,0 | 555,7 | ||
| ВZ2 =9,4∙10-3 Е, Тл | 0,63 | 1,25 | 1,37 | 1,5 | 1,63 |
| НZ2, А/м | |||||
| FZ2 =11,5∙10-3 НZ2, А | 3,45 | 10,8 | 15,5 | 26,1 | 54,6 |
| F δZ a = F δ+ FZ1+ Fa+ FZ2, А | |||||
| Фσ=2,83∙10-6 F δZ a , Вб | 0,0042 | 0,0089 | 0,0106 | 0,0138 | 0,0172 |
| Фm= Ф + Фσ=3,21∙10-4 Е + +2,83∙10-6 ∙F δZ a , Вб | 0,0255 | 0,0516 | 0,0575 | 0,065 | 0,0727 |
| Вm =8,97∙10-3 Е +7,9∙10-5 ∙F δZ a ,Тл | 0,714 | 1,44 | 1,61 | 1,82 | 2,04 |
| Нm, А/м | |||||
| Fm =0,181∙ Нm, А | 67,0 | ||||
| Fδmj = 250 Вm, A | |||||
| В j =7,26∙10-3 Е +6,4∙10-5 F δZ a , Тл | 0,57 | 1,16 | 1,3 | 1,47 | 1,63 |
| Нj, А/м | |||||
| Fj = 6,63∙10-2 Нj , А | 43,0 | 80,0 | |||
| Fm j= Fm + Fδmj+ Fj, А | |||||
| F вo= F δZo+ Fm+ Fδmj+ Fj, А | |||||
| F вo* | 0,45 | 1,22 | 1,78 | 2,68 | |
| Ф m * | 0,595 | 1,2 | 1,34 | 1,52 | 1,70 |
| F δZ a* | 0,38 | 0,809 | 0,95 | 1,245 | 1,55 |
| Fmj * | 0,07 | 0,19 | 0,26 | 0,54 | 1,123 |
| Фσ* | 0,098 | 0,208 | 0,248 | 0,323 | 0,402 |
Для магнитопровода статора выбираем сталь 1511 толщиной 0,5 мм. Полюсы ротора выполняем из стали Ст3 толщиной
1 мм. Толщину обода (ярма ротора) принимаем hj =0,05 м.
57. Магнитный поток в зазоре
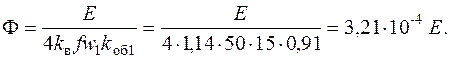
По рис. 1.2 при δм/δ=1,5; α=0,7; δ/τ=0,003/0,242=0,0124 находим k в=1,14 и αδ=0,66.
58. Уточненное значение расчетной длины статора
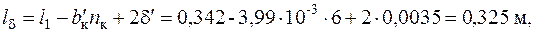
где b 'к=γδ=1,33·3·10-3=3,99·10-3;
γ= (b к/δ)2/(5+ b к/δ)=(1·10-2/3·10-3)2/(5+1·10-2/3·10-3) = 1,33.
59. Индукция в воздушном зазоре
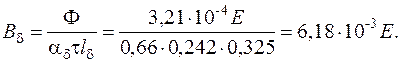
60. Коэффициент воздушного зазора статора
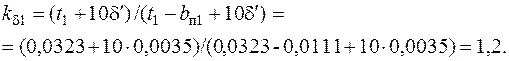
61. Коэффициент воздушного зазора ротора
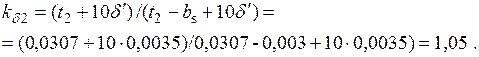
62. Результирующий коэффициент воздушного зазора
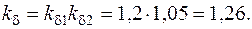
63. Магнитное напряжение воздушного зазора
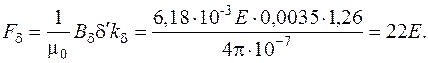
64. Ширина зубца статора по высоте 1/3 h′ п1 от его коронки
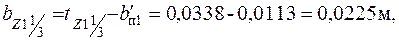
где 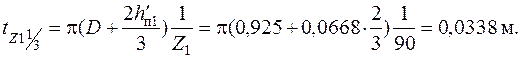
65. Индукция в сечении зубца по высоте 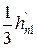 от его коронки
от его коронки
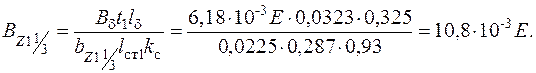
66. Магнитное напряжение зубцов статора
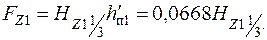
При Е =1,3 Е н 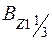 =1,87 > 1,8 Тл, поэтому соответствующую напряженность
=1,87 > 1,8 Тл, поэтому соответствующую напряженность 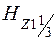 определяем по кривым намагничивания, рис. 7.1, с учётом коэффициента
определяем по кривым намагничивания, рис. 7.1, с учётом коэффициента
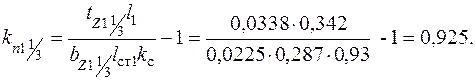
67. Индукция в спинке статора
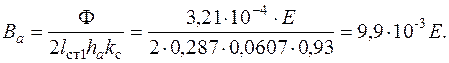
68. Магнитное напряжение спинки статора
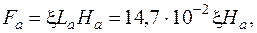
где 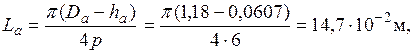
ξ определяем по рис. 7.2.
69. Высота зубца ротора
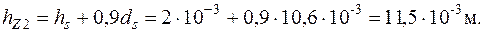
70. Расчетная ширина зубца ротора (для круглых пазов)
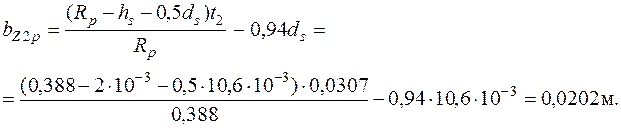
71. Индукция в зубце ротора
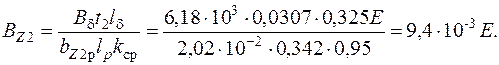
72. Магнитное напряжение зубцов ротора
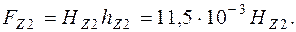
73. Удельная магнитная проводимость рассеяния между внутренними поверхностям сердечников полюсов
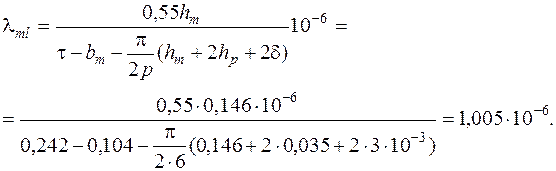
74. Удельная магнитная приводимость рассеяния между внутренними поверхностями полюсных наконечников
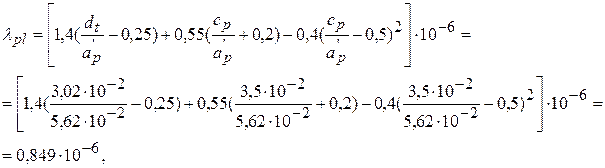
где 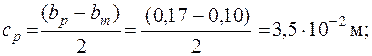
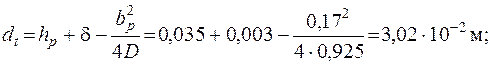
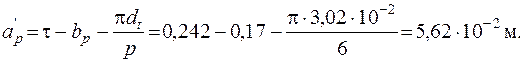
75. Удельная магнитная проводимость рассеяния между торцевыми поверхностями
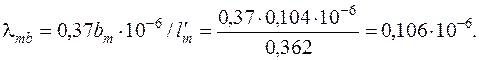
76. Удельная магнитная проводимость для потока рассеяния
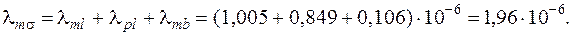
77. Магнитное напряжение ярма статора, зазора и зубцов полюсного наконечника, А,
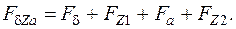
78. Поток рассеяния полюса, Вб,
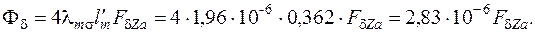
79. Поток в сечении полюса у его основания, Вб,
Ф m =Ф+Фσ=3,21∙10-4 Е +2,83∙10-6 F δ Za .
80. Индукция в полюсе, Тл,
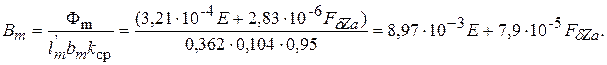 Так как при Е от 1,1 U н до 1,3 U н Вm >1,6 Тл, то в табл. 3 расчёт падения магнитного напряжения на полюсе Fm производим по эквивалентной напряженности Нmр, которую определяем по трем сечениям полюса, табл. 4.
Так как при Е от 1,1 U н до 1,3 U н Вm >1,6 Тл, то в табл. 3 расчёт падения магнитного напряжения на полюсе Fm производим по эквивалентной напряженности Нmр, которую определяем по трем сечениям полюса, табл. 4.
Таблица 4
| Е * | Ф m | Ф' m | Ф m cp | Bm | B'm | Вm cp | Нm | Н'm | Нm cp | Нmр |
| 1,1 | 0,0575 | 0,0515 | 0,0544 | 1,61 | 1,44 | 1,53 | ||||
| 1,2 | 0,065 | 0,0573 | 0,0611 | 1,82 | 1,61 | 1,72 | ||||
| 1,3 | 0,0727 | 0,0629 | 0,0676 | 2,04 | 1,76 | 1,9 |
При этом Ф m =Ф+Фσ; Ф' m =Ф+Фσλ pl /λ m σ=Ф+0,43Фσ;
Ф m cp=(Ф m +Ф' m)/2; 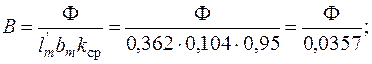
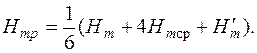
81. Магнитное поле напряжения полюса, А,
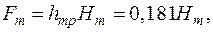
где hmp=hm+hp= 0,146+0,035=0,181 м.
82. Магнитное напряжение стыка между полюсом и ярмом ротора, А,
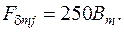
83. Индукция в ярме ротора, Тл,
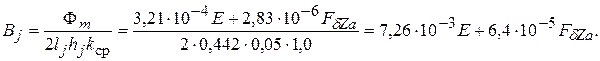
84. Магнитное напряжение в ярме ротора, А,
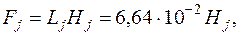
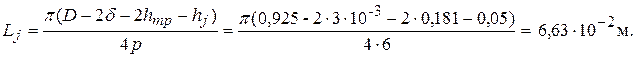 85. Магнитное напряжение сердечника полюса, ярма ротора и стыка между полюсом и ярмом, А,
85. Магнитное напряжение сердечника полюса, ярма ротора и стыка между полюсом и ярмом, А,
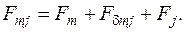
86. Магнитодвижущая сила обмотки возбуждения на полюс, А,
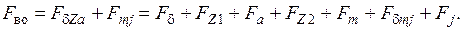
Результаты расчета магнитной цепи сводим в табл. 3. При переводе значений FδZa, Fmj, Ф m в относительные единицы за базовые соответственно приняты F во и Ф при Е *=1.
По табл. 3 на рис. 4 строим в относительных единицах характеристику холостого хода.
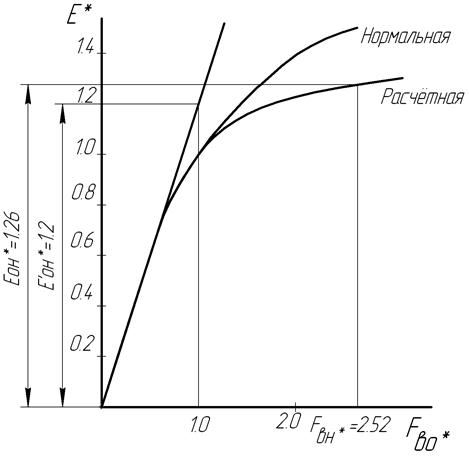
Рис. 4. Характеристика холостого хода
На этом же рис. 4 приведена нормальная (типовая) характеристика холостого хода.
 2015-03-20
2015-03-20 490
490








