Пусть задана для участника 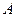 матрица выигрышей
матрица выигрышей 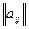 , которую называют платежной матрицей.
, которую называют платежной матрицей.
Рассмотрим решение матричных игр данного класса на следующем примере:
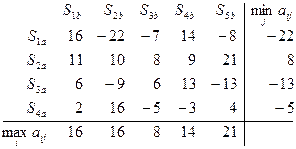
Определение 1 (доминирующая стратегия). Если для двух стратегий 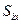 и
и 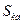 выполняется условие
выполняется условие 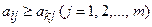 , и существует хотя бы одна стратегия
, и существует хотя бы одна стратегия 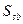 такая, что
такая, что 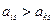 , тогда
, тогда 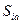 является доминирующей стратегией по отношению к
является доминирующей стратегией по отношению к 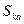 , а чистая стратегия
, а чистая стратегия 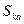 – доминируемой стратегией.
– доминируемой стратегией.
Если для пары стратегий 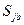 и
и 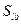
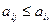
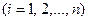 , и существует
, и существует 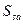 такая, что
такая, что 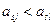 , тогда
, тогда 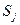 – доминирующая по отношению к
– доминирующая по отношению к 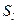 , а
, а 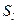 – доминируемая стратегия.
– доминируемая стратегия.
Доминируемые стратегии можно исключить из матрицы 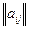 , так как оптимального решения среди них не будет.
, так как оптимального решения среди них не будет.
Выбираем оптимальную стратегию 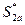 для участника А по принципу:
для участника А по принципу:
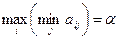 .
.
Величина 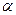 определяет нижнюю цену игры. Выбор стратегии по этому принципу гарантирует, что выигрыш будет не меньше, чем
определяет нижнюю цену игры. Выбор стратегии по этому принципу гарантирует, что выигрыш будет не меньше, чем 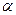 .
.
Для участника B оптимальная стратегия 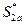 определяется по принципу:
определяется по принципу: 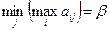 – верхняя цена игры.
– верхняя цена игры.
Игры, у которых 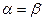 , называются играми с седловой точкой.
, называются играми с седловой точкой.
Отметим, что всегда 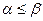 . Действительно, пусть
. Действительно, пусть 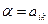 и
и 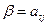 :
:
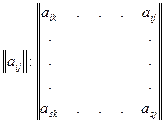
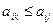 , так как
, так как 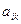 – минимальное в строке
– минимальное в строке 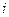 ;
; 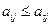 , так как
, так как 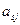 – максимальное в столбце
– максимальное в столбце 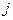 , откуда следует, что
, откуда следует, что 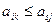 .
.
Может быть несколько седловых точек, тогда цена игры во всех этих точках одинакова: 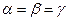 , где
, где 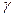 – цена игры.
– цена игры.
Пусть существуют две седловые точки 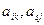 . Из условий определения седловых точек следует:
. Из условий определения седловых точек следует:
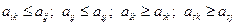 .
.
Все эти нестрогие неравенства выполняются только в случае, когда все 4 числа равны: 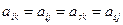 .
.
 2015-03-07
2015-03-07 365
365







