Выражение вида 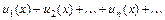 , где
, где 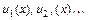 - последовательность функций, определённых на одном и том же множестве
- последовательность функций, определённых на одном и том же множестве 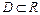 , называется функциональным рядом, определённым на
, называется функциональным рядом, определённым на 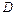 и обозначается
и обозначается 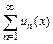 . Функция
. Функция 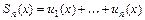 называется
называется 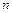 -ой частичной суммой функционального ряда.
-ой частичной суммой функционального ряда.
Точка 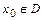 , в которой сходится числовой ряд
, в которой сходится числовой ряд 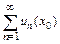 , называется точкой сходимости функционального ряда. Множество
, называется точкой сходимости функционального ряда. Множество 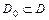 , состоящее из всех точек сходимости функционального ряда, называется его областью сходимости. Область
, состоящее из всех точек сходимости функционального ряда, называется его областью сходимости. Область 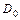 сходимости функционального ряда обычно уже, чем область его определения
сходимости функционального ряда обычно уже, чем область его определения 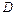 .
.
Ряд 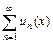 называется абсолютно сходящимся на множестве
называется абсолютно сходящимся на множестве 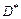 , если при всех
, если при всех 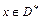 сходится ряд
сходится ряд 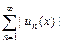 . Всякий ряд, абсолютно сходящийся на множестве
. Всякий ряд, абсолютно сходящийся на множестве 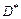 , сходится на этом множестве. Область
, сходится на этом множестве. Область 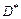 абсолютной сходимости ряда обычно уже его области сходимости
абсолютной сходимости ряда обычно уже его области сходимости 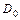 .
.
Функцию 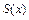 , определённую в области сходимости
, определённую в области сходимости 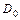 функционального ряда такую, что при любом фиксированном
функционального ряда такую, что при любом фиксированном 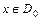
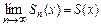 , называют суммой ряда и пишут
, называют суммой ряда и пишут 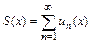 . При
. При 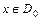 остаток ряда представляет собой также функцию
остаток ряда представляет собой также функцию 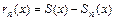 , где
, где 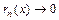 при
при 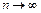 и при любом
и при любом 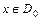 .
.
Для нахождения области сходимости ряда 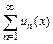 применяют известные признаки сходимости числовых рядов, считая
применяют известные признаки сходимости числовых рядов, считая 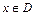 фиксированным.
фиксированным.
В частности, на основании признаков Даламбера и Коши (радикального) можно утверждать, что ряд сходится (и притом абсолютно), если 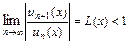 и
и 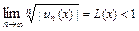 , соответственно, и расходится, если
, соответственно, и расходится, если 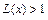 . В точках
. В точках 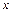 , в которых
, в которых 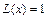 , сходимость ряда исследуют с помощью других признаков (например, признаков сравнения, интегрального признака Коши, признака Лейбница).
, сходимость ряда исследуют с помощью других признаков (например, признаков сравнения, интегрального признака Коши, признака Лейбница).
В задачах 8.125-8.139 найти области сходимости следующих функциональных рядов:
8.125 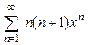 . 8.126
. 8.126 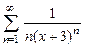 . 8.127
. 8.127 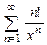 .
.
8.128 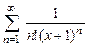 . 8.129
. 8.129 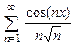 . 8.130
. 8.130 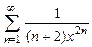 .
.
8.131 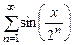 . 8.132
. 8.132 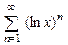 . 8.133
. 8.133 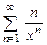 .
.
8.134 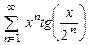 . 8.135
. 8.135 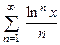 . 8.136
. 8.136 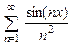 .
.
8.137 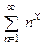 . 8.138
. 8.138 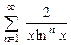 . 8.139
. 8.139 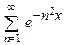 .
.
 2015-03-20
2015-03-20 226
226








