ГЛАВА 8. РЯДЫ.
Выражение вида 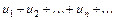 , где
, где 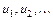 - последовательность чисел, называется числовым рядом и обозначатся
- последовательность чисел, называется числовым рядом и обозначатся 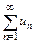 . Ряд
. Ряд 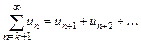 называется остатком
называется остатком 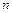 -ого порядка исходного ряда и обозначается
-ого порядка исходного ряда и обозначается 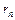 . Сумма
. Сумма 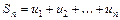
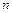 первых членов ряда называется
первых членов ряда называется 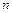 -ой частичной суммой ряда.
-ой частичной суммой ряда.
Ряд 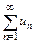 называется сходящимся, если существует конечный предел
называется сходящимся, если существует конечный предел 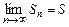 и расходящимся, если предел не существует. Число
и расходящимся, если предел не существует. Число 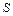 называется суммой сходящегося ряда, при этом пишут
называется суммой сходящегося ряда, при этом пишут 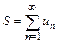 . Одновременно с рядом
. Одновременно с рядом 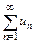 сходится и расходится его остаток
сходится и расходится его остаток 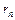 . В случае сходящегося ряда его остаток записывают в виде
. В случае сходящегося ряда его остаток записывают в виде 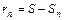 .
.
Сходимость или расходимость ряда не нарушится, если прибавить или отбросить конечное число его членов.
Если ряд 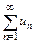 сходится, то
сходится, то 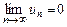 (необходимый признак сходимости ряда). Обратное утверждение неверно.
(необходимый признак сходимости ряда). Обратное утверждение неверно.
Если 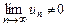 , то ряд
, то ряд 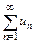 расходится (достаточный признак расходимости ряда).
расходится (достаточный признак расходимости ряда).
Признак сравнения. Если для рядов 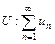 и
и 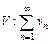 , начиная с некоторого
, начиная с некоторого 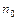 , для всех
, для всех 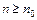 выполняется условие
выполняется условие 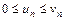 , то из сходимости ряда
, то из сходимости ряда 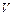 следует сходимость ряда
следует сходимость ряда 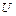 , из расходимости ряда
, из расходимости ряда 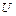 следует расходимость ряда
следует расходимость ряда 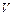 .
.
Предельный признак сравнения. Еслисуществует конечный и отличный от нуля предел 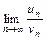 (в частности, если
(в частности, если 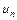 ~
~ 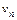 при
при 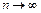 ), то ряды
), то ряды 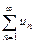 и
и 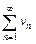 (
(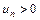 ,
, 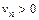 начиная с некоторого
начиная с некоторого 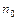 ) сходятся или расходятся одновременно.
) сходятся или расходятся одновременно.
Для применения признаков сравнения необходимо наличие «эталонных» рядов, сходимость или расходимость которых известна. В качестве «эталонных» рядов широко используются: 1) обобщённый гармонический ряд 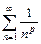 , который сходится при
, который сходится при 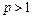 и расходится при
и расходится при 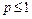 ; 2) геометрический ряд
; 2) геометрический ряд 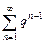 , который сходится при
, который сходится при 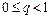 , при этом его сумма равна
, при этом его сумма равна 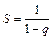 и расходится при
и расходится при 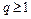 . Таким образом, для применения признаков сравнения нужно найти последовательность
. Таким образом, для применения признаков сравнения нужно найти последовательность 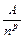 или
или 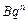 , где
, где 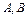 - некоторые числа, такую, что
- некоторые числа, такую, что 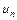 ~
~ 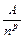 или
или 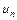 ~
~ 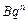 при
при 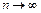 .
.
Полезно иметь в виду эквивалентности (при 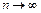 ,
, 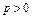 ):
):
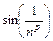 ~
~ 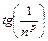 ~
~ 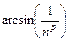 ~
~ 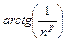 ~
~ 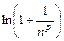 ~
~ 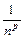 ,
,
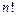 ~
~ 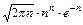 ,
,
а также оценки 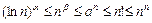 (
(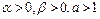 ), имеющие место, начиная с некоторого
), имеющие место, начиная с некоторого 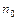 , для всех
, для всех 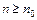 .
.
В задачах 8.1-8.9 показать, что следующие ряды сходятся, и найти их суммы:
8.1 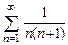 . 8.2
. 8.2 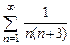 . 8.3
. 8.3 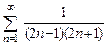 .
.
8.4 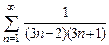 . 8.5
. 8.5 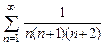 . 8.6
. 8.6 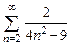 .
.
8.7 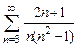 . 8.8
. 8.8 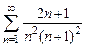 . 8.9
. 8.9 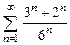 .
.
В задачах 8.10-8.18 используя необходимый признак сходимости ряда, установить расходимость следующих рядов:
8.10 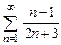 . 8.11
. 8.11 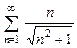 . 8.12
. 8.12 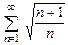 .
.
8.13 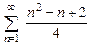 . 8.14
. 8.14 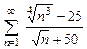 . 8.15
. 8.15 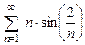 .
.
8.16 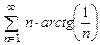 . 8.17
. 8.17 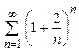 . 8.18
. 8.18 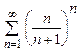 .
.
В задачах 8.19-8.46 используя признаки сравнения, исследовать на сходимость следующие ряды:
8.19 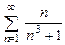 . 8.20
. 8.20 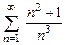 . 8.21
. 8.21 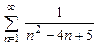 .
.
8.22 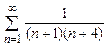 . 8.23
. 8.23 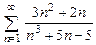 . 8.24
. 8.24 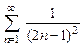 .
.
8.25 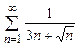 . 8.26
. 8.26 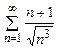 . 8.27
. 8.27 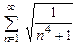 .
.
8.28 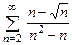 . 8.29
. 8.29 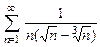 . 8.30
. 8.30 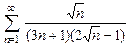 .
.
8.31 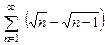 . 8.32
. 8.32 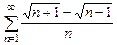 .
.
8.33 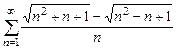 . 8.34
. 8.34 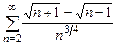 .
.
8.35 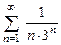 . 8.36
. 8.36 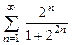 . 8.37
. 8.37 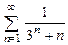 .
.
8.38 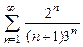 . 8.39
. 8.39 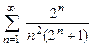 . 8.40
. 8.40 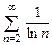 .
.
8.41 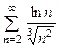 . 8.42
. 8.42 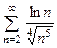 . 8.43
. 8.43 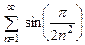 .
.
8.44 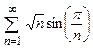 . 8.45
. 8.45 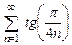 . 8.46
. 8.46 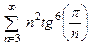 .
.
Признак Даламбера. Если для ряда 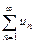 (
(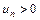 начиная с некоторого
начиная с некоторого 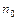 )
) 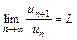 , то ряд сходится при
, то ряд сходится при 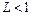 и расходится при
и расходится при 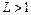 . Если
. Если 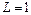 , то ряд может сходится или расходится; в этом случае его сходимость исследуется с помощью других признаков.
, то ряд может сходится или расходится; в этом случае его сходимость исследуется с помощью других признаков.
В задачах 8.47-8.62 используя признак Даламбера, исследовать сходимость следующих рядов:
8.47 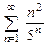 . 8.48
. 8.48 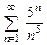 . 8.49
. 8.49 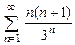 . 8.50
. 8.50 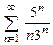 . 8.51
. 8.51 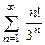 . 8.52
. 8.52 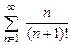 . 8.53
. 8.53 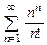 . 8.54
. 8.54 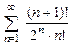 . 8.55
. 8.55 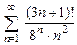 . 8.56
. 8.56 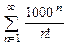 . 8.57
. 8.57 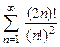 . 8.58
. 8.58 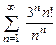 .
.
8.59 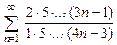 . 8.60
. 8.60 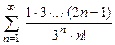 .
.
8.61 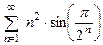 . 8.62
. 8.62 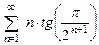 .
.
Признак Коши (радикальный). Если для ряда 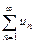 (
(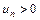 начиная с некоторого
начиная с некоторого 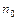 )
) 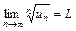 , то ряд сходится при
, то ряд сходится при 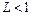 и расходится при
и расходится при 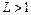 . Если
. Если 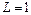 , то ряд может сходится или расходится; в этом случае его сходимость исследуется с помощью других признаков.
, то ряд может сходится или расходится; в этом случае его сходимость исследуется с помощью других признаков.
При применении признака Коши полезно иметь в виду, что: 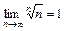 ,
, 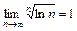 ,
, 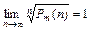 , где
, где 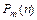 - многочлен порядка
- многочлен порядка 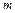 относительно
относительно 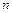 .
.
В задачах 8.63-8.74 используя радикальный признак Коши, исследовать сходимость следующих рядов:
8.63 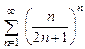 . 8.64
. 8.64 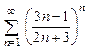 . 8.65
. 8.65 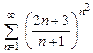 .
.
8.66 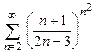 . 8.67
. 8.67 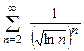 . 8.68
. 8.68 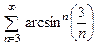 . 8.69
. 8.69 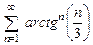 . 8.70
. 8.70 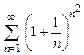 . 8.71
. 8.71 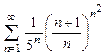 . 8.72
. 8.72 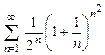 . 8.73
. 8.73 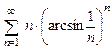 . 8.74
. 8.74 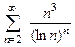 .
.
Интегральный признак Коши. Если 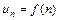 , где функция
, где функция 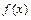 положительна, монотонно убывает и непрерывна при
положительна, монотонно убывает и непрерывна при 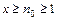 , то ряд
, то ряд 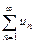 и интеграл
и интеграл 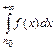 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
В задачах 8.75-8.80 используя интегральный признак Коши, исследовать сходимость следующих рядов:
8.75 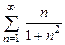 . 8.76
. 8.76 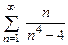 . 8.77
. 8.77 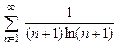 .
.
8.78 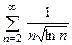 . 8.79
. 8.79 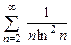 . 8.80
. 8.80 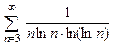 .
.
В задачах 8.81-8.100 исследовать сходимость рядов:
8.81 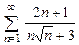 . 8.82
. 8.82 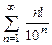 . 8.83
. 8.83 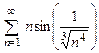 .
.
8.84 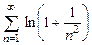 . 8.85
. 8.85 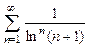 . 8.86
. 8.86 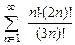 .
.
8.87  . 8.88
. 8.88 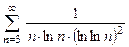 .
.
8.89 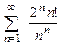 . 8.90
. 8.90 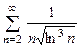 . 8.91
. 8.91 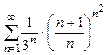 .
.
8.92 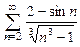 . 8.93
. 8.93 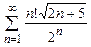 . 8.94
. 8.94 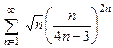
8.95 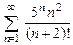 . 8.96
. 8.96 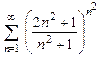 8.97
8.97 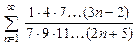
8.98 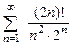 . 8.99
. 8.99 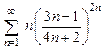 . 8.100
. 8.100 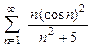 .
.
Ряд 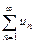 называется абсолютно сходящимся, если ряд
называется абсолютно сходящимся, если ряд 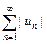 сходится. Сходящийся ряд
сходится. Сходящийся ряд 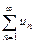 называется условно сходящимся, если ряд
называется условно сходящимся, если ряд 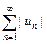 расходится.
расходится.
Сумма абсолютно сходящегося ряда не изменяется при перестановке членов ряда. Сумму условно сходящегося ряда путём перестановки его членов можно сделать равной любому числу.
Если ряд 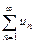 абсолютно сходится, то он является сходящимся (достаточный признак сходимости знакопеременного ряда).
абсолютно сходится, то он является сходящимся (достаточный признак сходимости знакопеременного ряда).
Для исследования ряда на абсолютную сходимость используют известные признаки сходимости знакоположительных рядов. В частности, ряд 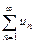 сходится абсолютно, если
сходится абсолютно, если 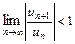 или
или 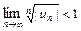 . В общем случае из расходимости ряда
. В общем случае из расходимости ряда 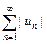 не следует расходимость ряда
не следует расходимость ряда 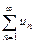 . Но если
. Но если  или
или 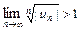 , то расходится не только ряд
, то расходится не только ряд 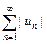 , но и ряд
, но и ряд 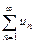 .
.
Ряд называется знакочередующимся, если все его соседние члены имеют разные знаки.
Признак Лейбница. Если для знакочередующегося ряда 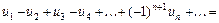
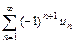 (
(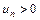 ) выполнены условия: 1)
) выполнены условия: 1) 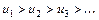 (может начать выполняться начиная с некоторого
(может начать выполняться начиная с некоторого 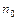 ); 2)
); 2) 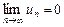 , то знакочередующийся ряд сходится (по крайней мере условно). Для остатка ряда
, то знакочередующийся ряд сходится (по крайней мере условно). Для остатка ряда 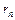 в этом случае справедлива оценка
в этом случае справедлива оценка 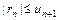 .
.
Сумму знакочередующегося ряда с заданной степенью точности 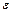 вычисляют по приближённой формуле
вычисляют по приближённой формуле 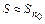
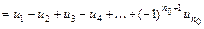 , где
, где 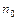 - минимальный из номеров
- минимальный из номеров 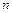 , для которых
, для которых 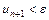 .
.
В задачах 8.101-8.120 исследовать на абсолютную и условную сходимость следующие ряды:
8.101  . 8.102
. 8.102 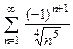 . 8.103
. 8.103 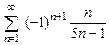 .
.
8.104 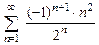 8.105
8.105 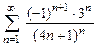 8.106
8.106 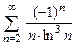 .
.
8.107 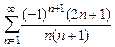 8.108
8.108 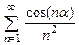 8.109
8.109 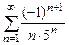 .
.
8.110 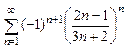 . 8.111
. 8.111 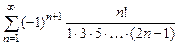 .
.
8.112 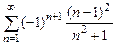 . 8.113
. 8.113 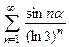 . 8.114
. 8.114 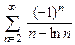 .
.
8.115 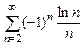 . 8.116
. 8.116 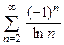 . 8.117
. 8.117 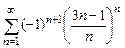 .
.
8.118 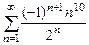 . 8.119
. 8.119 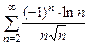 . 8.120
. 8.120 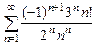 .
.
В задачах 8.121-8.124 вычислить сумму ряда с точностью до 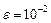 . Сколько членов ряда следует для этого взять?
. Сколько членов ряда следует для этого взять?
8.121 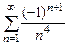 8.122
8.122 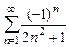 8.123
8.123 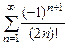 8.124
8.124 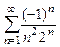 .
.
 2015-03-20
2015-03-20 568
568







