Постановка задачи целочисленного программирования

Значительная часть экономических задач, относящихся к ЗЛП, требует целочисленного решения, К ним относятся задачи, у которых переменные величины означают количество единиц неделимой продукции, например: выпуск оборудования, распределение производственных заданий между предприятиями, распределение самолетов по линиям и т.д.

В общем виде математическая модель задачи целочисленного программирования имеет вид:

Определить максимальное (минимальное) значение функции:

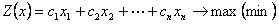
при ограничениях

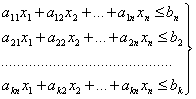
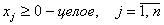
Иногда можно получить целочисленное решение, не прибегая к специальным вычислительным приемам. Такой особенностью обладает, например, транспортная задача. Но зачастую оптимальное решение задачи, найденное симплексным методом, не является целочисленным. Его можно округлить до ближайших целых чисел. Однако такое округление может дать решение, не лучшее среди целочисленных решений, или привести к решению, не удовлетворяющему системе ограничений. Для решения задач ЦП разработан ряд вычислительных методов.

При наличии в задаче линейного программирования двух переменных, а в системе ограничений – неравенств она может быть решена графическим методом.

В системе координат Х₁ОХ₂ находят область допустимых решений, строят вектор 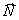и линии уровня. Перемещая линию уровня по направлению 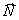для задач на максимум (минимум) находим наиболее удаленную (приближенную) от начала координат точку и ее координаты.

В том случае, когда координаты этой точки нецелочисленные, в области допустимых решений строят целочисленную решетку и находят на ней такие целые числа, которые удовлетворяют системе ограничений и при которых значения целевой функции наиболее близко к экстремальному нецелочисленному решению. Координаты такой вершины и являются целочисленным решением.

2. Определение оптимального плана задачи целочисленного программирования (метод Гомори).

Одним из основных методов решения задач целочисленного программирования является метод Гомори. Вначале симплексным методом находят оптимальное решение задачи. Если решение целочисленное, то задача решена. Если же оно содержит хотя бы одну дробную координату, то накладывают дополнительное ограничение по целочисленности и вычисления продолжают до получения нового решения. Если и оно является нецелочисленным, то вновь накладывают дополнительное ограничение по целочисленности. Вычисления продолжают до тех пор, пока не будет получено целочисленное решение или показано, что задача не имеет целочисленного решения.

Пусть получено оптимальное решение 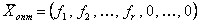, которое не является целочисленным, тогда последняя симплекс таблица имеет вид:

Базис	СБаз.	В	С1	С2	…	Сr	Сr+1	…	Cn
	х1	х2	…	хr	хr+1	…	хn
х1	C1	b1			…		h1,r+1	…	h1n
х2	C2	b2			…		h2,r+1	…	h2n
…	…	…	…	…	…	…	…	…	…
xr	Cr	br			…		hr,r+1	…	hrn
Δj	Z(х0)			…		Δr+1	…	Δn

Пусть 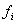и хотя бы одно 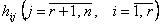- дробные числа.

Введем следующие обозначения 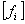и 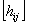целые части чисел 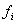и .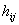

Определение. Целой частью числа 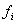называют наибольшее целое число, не превосходящее числа .

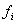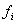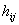Дробную часть чисел и обозначим 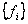и , она определяется следующим образом:

,

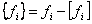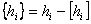
Примеры:

Если 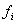и хотя бы одно 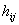- дробны, то с учетом введенных обозначений дополнительной ограничение по целочисленности примет вид:

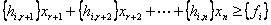
Данное ограничение вводится в последнюю симлекс таблицу и решение задачи продолжается дальше.

Примечание. 1) Если 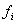- дробное число, а все 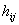- целые числа, то задача линейного программирования не имеет целочисленного решения.

2) Ограничение целочисленности может быть наложено не на все переменные, а лишь на их часть. В этом случае задача является частично целочисленной.

1.Понятие об игровых моделях.

Главная задача управленческого персонала любой компании – принятие правильного решения вовремя. Такого рода задачи встречаются во многих сферах человеческой деятельности: в экономике, в политике, в военном деле и др. Довольно часто приходится принимать решения в условиях неопределенности, а именно, возникают ситуации, в которых две (или более) стороны преследуют различные цели, а результаты любого действия каждой из сторон зависят от мероприятий партнера. Например:

1) доход производителя некоторого продукта зависит не только от цены на этот продукт, но и от того, сколько продукта решит купить покупатель по данной цене;

2) при выборе ассортимента товаров, выпускаемых данным предприятием, необходимо учитывать, какой ассортимент товаров будут выпускать другие предприятия. Иначе может оказаться, что товары, выпущенные данным предприятием, не найдут сбыта;

Все ситуации, когда эффективность действия одного участника не зависит от действия других участников, можно разделить на два типа:

1) ситуации, когда интересы участников совпадают. В этих случаях участники должны договориться между собой о совместных действиях;

2) ситуации, когда интересы участников не совпадают. Тогда им не выгодно сообщать друг другу свои решения, так как кто-либо из участников сможет воспользоваться значением чужих решений и получить больший выигрыш. Ситуации такого рода называются конфликтными.

Теория игр занимается построением математических моделей конфликтных ситуаций и разработкой методов решения возникающих в этих ситуациях задач.

Упрощенная модель конфликтной ситуации называется игрой, стороны, участвующие в конфликте – игроками, а исход конфликта – выигрышем.

В игре могут сталкиваться интересы двух или нескольких противников, поэтому игры разделяются на парные и множественные. Игра называется парной, если в ней участвуют два игрока, и множественной, если число игроков больше двух.

Если во множественной игре интересы игроков совпадают, то они могут объединяться, создавать коалиции. Такие игры называются коалиционными.

Наибольшее практическое значение имеют парные игры. Обозначим игроков через А и В. Предполагается, что результат игры (выигрыш) определяется некоторым числом.

Ходом игрока будем называть выбор одного из предложенных правилами игры действий и его осуществлением.

Стратегией игрока называется план, по которому он совершает выбор ходов в течение игры.

Задача теории игр – определение для игроков оптимальной стратегии, т.е. такой стратегии, которая при многократном повторении игры обеспечивает каждому игроку максимально возможный средний выигрыш.

Теория игр является современной, научной методикой принятия оптимальных решений в условиях противоречий, в условиях конфликта, в условиях неполного знания тех обстоятельств, в которых приходится принимать решение.

Рассмотрим простейшую математическую модель конфликтной ситуации, когда имеются два участника и когда выигрыш одного равен проигрышу другого. Такая модель называется антагонистической игрой двух лиц с нулевой суммой. Задача первого игрока – максимизировать свой выигрыш. Задача второго игрока – минимизировать свой проигрыш или минимизировать выигрыш первого игрока. Игру можно представить в виде матрицы, в которой строки – стратегии первого игрока, столбцы стратегии второго игрока, а элементы матрицы – выигрыши первого игрока. Такую матрицу называют платежной (или матрицей игры). В общем случае парную игру с нулевой суммой можно записать платежной матрицей.

Задача каждого из игроков – найти наилучшую стратегию игры, при этом предполагается, что противники одинаково разумны и каждый из них делает все, чтобы получить наибольший доход.

Найдем наилучшую стратегию первого игрока. Пусть игрок А выбирает некоторую стратегию А_i, тогда в наихудшем случае он получит выигрыш, равный 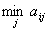. Предвидя такую возможность, игрок А должен выбирать такую стратегию, чтобы максимизировать свой минимальный выигрыш :

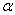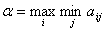
Величина 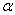-гарантированный выигрыш игрока А – называется нижней ценой игры. Стратегия обеспечивающая получение 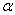называется максиминной.

Игрок В, выбирая стратегию, исходит из следующего принципа: при выборе некоторой стратегии В_j его проигрыш не превосходит максимального из значений элементов j-го столбца матрицы, т.е. меньше или равен 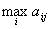. Поэтому игрок В, очевидно, выберет такое значение j, при котором его максимальный проигрыш 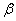минимизируется:

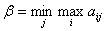
Величина 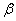называется верхней ценой игры, а соответствующая ему стратегия игрока – минимаксной.

Теорема. Нижняя цена игры всегда не превосходит верхней цены игры. .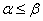

Если 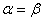, то такая игра называется игрой с седловой точкой, а пара оптимальных стратегий 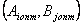- седловой точкой матрицы. Число 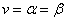называется ценой игры. Если игра имеет седловую точку, то говорят, что она решается в чистых стратегиях.

Решение игр в смешанных стратегиях:

Если игра не имеет седловой точки, то поиск решения игры приводит к применению сложной стратегии, состоящей в случайном применении двух и более стратегий с определенными частотами. Такая сложная стратегия называется смешанной.

Смешанной стратегией 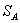игрока А называется применение им чистых стратегий 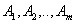с вероятностями 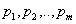соответственно, причем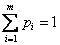

Аналогично определяется смешанные стратегии 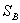игрока В, как применение чистых стратегий 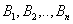с вероятностями 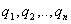соответственно, причем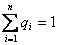

Основная теорема теории игр (Теорема Неймана).

Каждая конечная игра имеет по крайней мере одно оптимальное решение, возможно среди смешанных стратегий.

Если чистая стратегия применяется с отличной от нуля вероятностью, то она называется активной.

Теорема об активных стратегиях:

Если один из игроков придерживается своей активной стратегии, то выигрыш остается неизменным и равным цене игры v, если второй игрок не выходит за пределы своих активных стратегий.

Эта теорема имеет большое практическое значение – она дает конкретные модели нахождения оптимальных стратегий при отсутствии седловой точки.

Рассмотрим матричную игру 2x2. Платежная матрица такой игры имеет вид:

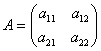
Если седловой точки нет, то решением являются смешанные стратегии 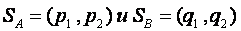, которые находятся из решения систем уравнений:

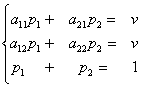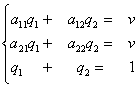(1) и (2)

Замечание. Для решения системы (2) достаточно выбрать два уравнения, т.к. после решения системы (1) цена игры v уже найдена. Можно взять первое и третье уравнения либо второе и третье уравнения. Матрицы большой размерности можно упростить, уменьшив их размерность путем вычеркивания дублирующих (одинаковых) и заведомо невыгодных стратегий.

2. Решение игр с помощью линейного программирования.

Каждая конечная игра двух лиц с нулевой суммой может быть представлена как задача линейного программирования.

Пусть игра mxn задана платежной матрицей

(1)

и не имеет седловой точки. Тогда для отыскания оптимальной стратегии игрока А рассмотрим систему

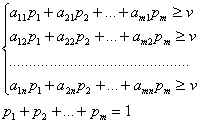(2)

Разделим на v>0 и обозначим 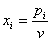, (i=1,2,…,m). (3)

Тогда имеем систему:

(4)

Игрок А стремится сделать свой гарантированный выигрыш v максимальным. Это значит, что величина 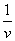должна принимать минимальное значение. Таким образом, задача решения игры свелась к следующей задаче линейного программирования: определить такие неотрицательные значения переменных х₁,х₂,..,х_m, чтобы обратилась в минимум линейная функция

Z=x₁+x₂+…+x_m

при условии, что выполняются ограничения (4).

Решая задачу симплекс методом находим х_i (i=1,2,..,m), Z= 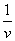, а затем p_i=v_ix_i.

Аналогично для игрока В получаем двойственную задачу линейного программирования:

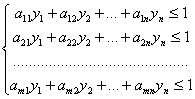(5)

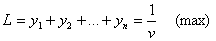, где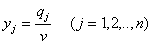

Итак, решение игры mxn свелось к решению двойственной пары задач линейного программирования. Согласно теоремам теории игр это решение всегда существует.

3.Критерии выбора решений в условиях неопределенности.

В рассмотренных ранее матричных играх предполагалось, что в них принимают участие два игрока, интересы которых противоположны. Поэтому действия каждого игрока направлены на увеличение выигрыша (уменьшения проигрыша). Однако в некоторых задачах, приводящих к игровым, имеется неопределенность, вызванная отсутствием информации об условиях, в которых осуществляется действие (погода, покупательский спрос и т.д.). Эти условия зависят не от сознательных действий другого игрока, а от объективной действительности, которую называют природой. Такие игры называются статистическими или играми «с природой».

Человек в играх с природой стремится действовать осмотрительно в зависимости от конкретной ситуации, природа действует случайно она безразлична к выигрышу, и не стремится использовать промахи игрока. Условия игры задаются матрицей. При выборе оптимальной стратегии игрока А применяются различные критерии принятия решения.

1. Критерий Байеса.

При известном распределении вероятностей различных состояний природы критерием принятия решения является максимум математического ожидания выигрыша, то есть

,

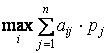где 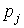– вероятности состояний природы, причем .

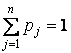2. Критерий Лапласа.

В некоторых задачах, когда вероятности состояний природы неизвестны, для их оценки используются принцип недостаточности основания Лапласа, согласно которому все состояния природы полагаются равновероятными.

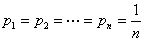
Критерием принятия решения является максимум математического ожидания выигрыша, то есть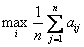

Если распределение вероятностей состояний природы неизвестно, то используются следующие критерии:

3. Максимальный критерий Вальда.

Он основан на выборе стратегии игрока А, при которой минимальный выигрыш максимален. Если руководствоваться этим критерием, надо ориентироваться на худшее в игре и выбирать ту стратегию, при которой выигрыш в худших условиях является максимальным:

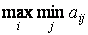
4. Критерий минимального риска Сэвиджа.

Стратегия выбирается из условия, чтобы не допустить чрезмерно высоких потерь, к которым она может привести. Находится матрица рисков, элементы которой показывают, какой убыток понесет игрок, если для каждого состояния природы он не выберет наилучшей стратегии. Оптимальная стратегии находится из выражения

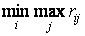
где .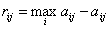

5. Критерий Гурвица

Выбирается стратегия, при которой достигается

,

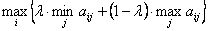где 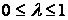- степень оптимизма

Замечание. Если 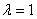, критерий Гурвица превращается в пессимистический критерий Вальда, а при 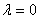- в критерий крайнего оптимизма, рассчитанный на наилучшее стечение обстоятельств. На 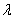оказывает влияние степень ответственности лица, принимающего решения по выбору стратегии. Чем хуже последствия ошибочных решений, больше желание застраховаться, тем ближе 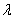к единице.

Мы не можем признать окончательное решение, выбранное по какому-либо одному критерию. Поэтому необходимо проанализировать решения, полученные по указанным критериям, и выбрать доминирующий ответ.