Алгоритм решения задач с помощью рекуррентных уравнений Беллмана

Рассмотрим последовательность задач, полагая последовательно n=1,2,… при различных состояниях s – одношаговую, двухшаговую и т.д., - используя принцип оптимальности.

На каждом шаге любого состояния системы s_k-1 решение X_k нужно выбирать «с оглядкой», так как этот выбор влияет на последующее состояние s_k и дальнейший процесс управления, зависящий от s_k. Это следует из принципа оптимальности.

Но есть один шаг, последний, который можно для любого состояния s_n-1планировать локально-оптимально, исходя только из соображений этого шага.

Рассмотрим n-й шаг: s_n-1 – состояние системы к началу n-го шага, 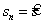- конечное состояние, X_n – управление на n-м шаге, а 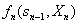- целевая функция (выигрыш) n-го шага.

Согласно принципа оптимальности, X_n нужно выбирать так, чтобы для любых состояний s_n-1 получить максимум (минимум) целевой функции на этом шаге.

Обозначим через 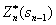максимум целевой функции – показателя эффективности n-го шага при условии, что к началу последнего шага система S была в произвольном состоянии s_n-1, а на последнем шаге управление было оптимальным.

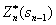называется условным максимумом целевой функции на n-м шаге.

Очевидно, что

Максимизация ведется по всем допустимым управлениям X_n.

Решение X_n, при котором достигается 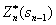, также зависит от s_n-1 и называется условным оптимальным управлением на n-м шаге. Оно обозначается через .

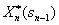Решив одномерную задачу локальной оптимизации, найдем для всех возможных состояний s_n-1 две функци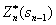и и .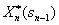

1.Общая задача нелинейного программирования.

Математическая модель задачи нелинейного программирования в общем виде формулируется следующим образом: найти вектор 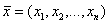, удовлетворяющий системе ограничений

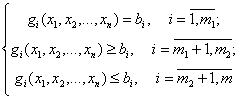
и доставляющий экстремум целевой функции

,

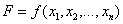где 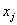- переменные;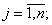 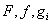- заданные функции от n переменных; 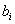- фиксированные значения.

Нелинейное программирование применяется при прогнозировании промышленного производства, управлении товарными ресурсами, планировании обслуживания и ремонта оборудования и т.д.

В зависимости от вида целевой функции и системы ограничений разрабатываются специальные методы решения, к которым относятсяметоды множителей Лагранжа, квадратичное и выпуклое программирование, градиентные методы, приближенные методы решения, графический метод.

2.Метод множителей Лагранжа.

Дана задача нелинейного программирования

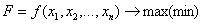
при ограничениях

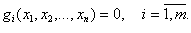
Предположим, что функци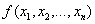и и 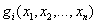непрерывны вместе со своими первыми частными производными.

Ограничения заданы в виде уравнений, поэтому для решения задачи воспользуемся методом отыскания условного экстремума функции нескольких переменных.

Составим функцию Лагранжа.

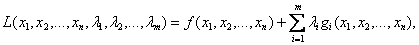
где 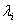- множители Лагранжа.

Найдем частные производные по каждой переменной.

, .

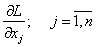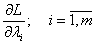Приравняв к нулю частные производные, получим систему

Решая систему, получим множество точек, в которых целевая функция может иметь экстремальные значения. Следует отметить, что условия рассмотренной системы являются необходимыми, но не достаточными. Поэтому не всякое полученное решение определяет точку экстремума целевой функции.

3.Выпуклое программирование.

В выпуклом программировании целевая функция является выпуклой (вогнутой) и гладкой.

Функция 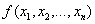называется выпуклой, если для любых х₁ и х₂ отрезок АВ, содержащие точки на кривой, лежит ниже графика функции и имеет место условие

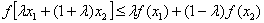
для любых х₁ и х₂ и любого действующего числа .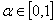

Если в данном условии изменить знак неравенства на противоположный, то получим определение вогнутой функции. Если же в условии неравенства выполняются как строгие, то функция называется строго выпуклой (или строго вогнутой).

Гладкость функции означает непрерывность её первых производных.

Задача выпуклого программирования формулируется следующим образом:

Найти минимум целевой функции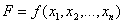

при наличии ограничений на переменные

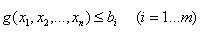
и условий неотрицательности переменных

.

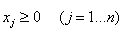Для вогнутой функции целевая функция достигает максимального значения.

К методам решения задач выпуклого программирования относятся: градиентные методы, в том числе метод наискорейшего спуска; метод секущих плоскостей; метод кусочно-линейной аппроксимации целевой функции и функции ограничений; графический метод при наличии двух переменных.

1.Поведение потребителя при выборе набора товаров.

Выбор товара потребителем определяется набором нужд покупателя (удобство, качество, надежность, скорость и т.д.), в соответствии с которыми и оценивается каждый конкретный продукт. Товар, получивший наивысшую оценку, воспринимается как наиболее выгодный и полезный. Таким образом, полезность, с точки зрения потребителя, это способность товара удовлетворять его потребности.

Полезность продукта, с точки зрения экономистов, индивидуальна для каждого потребителя. То, что полезно для одного человека, может быть абсолютно бесполезно для другого. В то время как физиологическая полезность одинакова для всех потребителей (за исключением потребителей с серьезными заболеваниями). Удовлетворяя жажду, Кока-Кола и столовая вода имеют одинаковую «экономическую» полезность (и тот и другой продукт удовлетворяет жажду), но разную физиологическую полезность.

«Экономическая» полезность индивидуальна и сложна для измерения. Кроме того, на сегодняшний день задача рационального потребительского выбора теряет свою актуальность. Предположим, хозяйка идет в магазин приобрести определенный набор продуктов для приготовления. Она не стоит перед выбором – купить мясо или рыбу, так как она уже определилась с меню. У нее возникает вопрос, какой сорт или какой фирмы производителя, купить тот или иной товар. А здесь мы уже обращаем внимание на качество товара.

Таким образом, в современных условиях развития рынка потребитель стремиться получить максимальное удовлетворение от потребления товаров высокого качества, с учетом своей покупательной способности.

Встает вопрос о построении математической модели задачи разумного потребительского выбора (направленного на потребление продуктов хорошего качества, не оказывающих на здоровье отрицательного влияния).

Такая задача имеет существенное преимущество в прикладном значении. В данном случае полезность не абстрактная величина, которая индивидуальна для каждого потребителя.

2.Функция полезности и ее свойства.

Пусть задана целевая функция предпочтения потребителя F(k₁x₁, k₂x₂,…, k_nx_n), где x_i – количество единиц i -го продукта, k_i – показатель качества единицы продукции.

Расчет показателя качества, предлагаемый нами, производится по формуле:

,

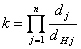где d_j – величина j -го параметра показателя качества по данным производителя,

d_Hj - величина j -го нормативного параметра показателя качества для образца продукта по медико-биологическим требованиям.

Учитывая, что потребитель ведет себя на рынке в соответствии со своей покупательной способностью, записываем бюджетное ограничение:

,

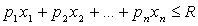где р₁, р₂,…, р_n – цены на продукты,

R – расходы на продовольственные товары.

Поскольку потребитель, приобретая набор продуктов питания, стремиться максимизировать полезность, то задача потребительского выбора сводится к следующей задаче на максимум:

F(k₁x₁, k₂x₂,…, k_nx_n)→max

при условиях

,

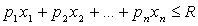х₁≥0, х₂≥0,…, х_n≥0

Полученная задача является задачей нелинейного программирования и решается методом Лагранжа.