1. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов 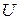 . Найти длину волны де Бройля для двух ситуаций: 1)
. Найти длину волны де Бройля для двух ситуаций: 1) 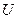 = 51 В; 2)
= 51 В; 2) 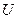 = 510 кВ.
= 510 кВ.
 Дано: Дано: 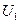 = 51 В; = 51 В; 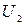 = 510 кВ; = 510 кВ; 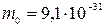 кг; кг; 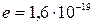 Кл Найти: Кл Найти: 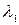 –? –? 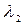 –? –? | Решение Длина волны де Бройля может быть выражена через импульс 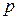 частицы и постоянную Планка частицы и постоянную Планка 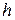 (смотри формулу (3.7)): (смотри формулу (3.7)): 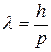 . Импульс частицы можно выразить через ее кинетическую энергию. При этом важно знать, . Импульс частицы можно выразить через ее кинетическую энергию. При этом важно знать, |
является частица классической или релятивистской. Для решения этого вопроса сравним в каждом случае кинетическую энергию частицы с энергией покоя
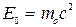 . (3.16)
. (3.16)
Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов 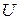 , может быть определена после умножения разности потенциалов на модуль заряда электрона
, может быть определена после умножения разности потенциалов на модуль заряда электрона 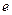 :
:
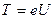 . (3.17)
. (3.17)
Вычисляя по формуле (3.17), получим:
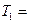 51 эВ =
51 эВ = 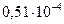 МэВ;
МэВ;
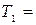
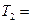 510 эВ = 0,51 МэВ.
510 эВ = 0,51 МэВ.
Энергию покоя электрона найдем по формуле (3.16):
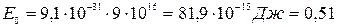 МэВ.
МэВ.
Очевидно, что 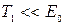 , а
, а 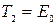 . Следовательно, в первой ситуации электрон является классической частицей, а во второй – релятивистской. Поэтому импульс электрона определим следующим образом:
. Следовательно, в первой ситуации электрон является классической частицей, а во второй – релятивистской. Поэтому импульс электрона определим следующим образом:
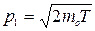 ; (3.18)
; (3.18)
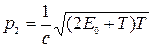 . (3.19)
. (3.19)
С учетом формул (3.18) и (3.19) представим формулу (3.7) в форме, удобной для выполнения вычислений:
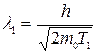 ; (3.20)
; (3.20)
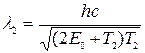 . (3.21)
. (3.21)
Вычислим длину волны де Бройля по формулам (3.20) и (3.21) с учетом найденных ранее значений кинетической энергии электрона:
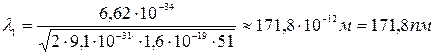 ;
;
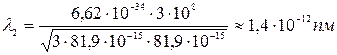 .
.
Ответы: 171,8 пм; 1,4 пм.
2. На узкую щель шириной а = 1 мкм направлен параллельный пучок электронов, имеющих скорость 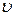 = 3,65 Мм/с. Учитывая волновые свойства электронов, определите расстояние х между двумя максимумами интенсивности первого порядка в дифракционной картине, полученной на экране, отстоящем на
= 3,65 Мм/с. Учитывая волновые свойства электронов, определите расстояние х между двумя максимумами интенсивности первого порядка в дифракционной картине, полученной на экране, отстоящем на 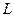 = 10 см от щели.
= 10 см от щели.
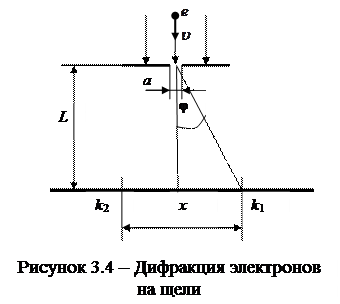
 Дано: Дано: 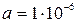 м; м; 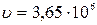 м/с; м/с; 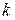 1 = 1; k 2 = -1; 1 = 1; k 2 = -1; 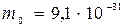 кг Найти: кг Найти: 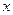 -? -? | Решение Изобразим схему дифракции электронов на щели (рисунок 3.4), укажем на ней положения дифракционных максимумов 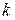 1 и k 2, ширину щели 1 и k 2, ширину щели 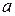 , угол дифракции , угол дифракции 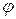 , искомое расстояние , искомое расстояние 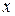 , расстояние , расстояние 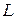 от плоскости диафрагмы до экрана. от плоскости диафрагмы до экрана. |
Воспользуемся оптико-механической аналогией и учтем, что при дифракции на щели положение дифракционных максимумов приблизительно можно определить по формуле
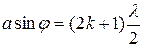 , (3.22)
, (3.22)
где k = 0, 1, 2, 3, …(в рассматриваемой ситуации следует выбрать k = 1), 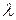
 - длина волны, которую следует сопоставить электрону, то есть длина волны де Бройля, определяемая по формуле (3.7).
- длина волны, которую следует сопоставить электрону, то есть длина волны де Бройля, определяемая по формуле (3.7).
Так как заданная в условии задачи скорость электрона значительно меньше скорости света в вакууме, то электрон можно считать нерелятивистской частицей, а его импульс определять по формуле:
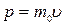 , (3.23)
, (3.23)
где 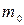 - масса покоя электрона,
- масса покоя электрона, 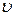 - скорость его движения.
- скорость его движения.
Так как рассматривается дифракция в первый порядок, то угол дифракции мал, и можно считать, что
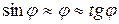 . (3.24)
. (3.24)
Тангенс угла дифракции найдем, воспользовавшись схемой опыта:
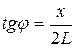 , (3.25)
, (3.25)
где 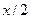 - расстояние от центра дифракционной картины до рассматриваемого максимума.
- расстояние от центра дифракционной картины до рассматриваемого максимума.
Комбинируя формулы (3.7),(3.22) – (3.25) с учетом значения k = 1, получим выражение для расчета расстояния между указанными в задаче дифракционными максимумами:
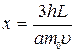 . (3.26)
. (3.26)
Вычислим искомое расстояние по формуле (3.26):
 .
.
Ответ: х = 60 мкм.
3 На грань кристалла никеля падает параллельный пучок электронов. Кристалл поворачивают так, что угол скольжения 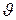 изменяется. Когда этот угол становится равным 64°, наблюдается максимальное отражение электронов, соответствующее дифракционному максимуму первого порядка. Принимая расстояние
изменяется. Когда этот угол становится равным 64°, наблюдается максимальное отражение электронов, соответствующее дифракционному максимуму первого порядка. Принимая расстояние 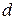 между атомными плоскостями кристалла равным 200 пм, определите длину волны де Бройля
между атомными плоскостями кристалла равным 200 пм, определите длину волны де Бройля 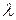 электронов и их скорость
электронов и их скорость 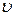 .
.
 Дано: Дано: 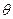 = 640; k = 1; d = 200 пм Найти: = 640; k = 1; d = 200 пм Найти: 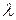 -? -? 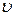 -? -? | Решение Воспользуемся для решения задачи формулой Вульфа-Брэгга, которая применима здесь, как и при дифракции рентгеновского излучения на кристалле: 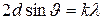 , (3.27) где , (3.27) где 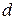 – постоянная кристаллической решетки, – постоянная кристаллической решетки, 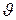 – угол скольжения, – угол скольжения, 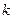 – порядок дифракции, – порядок дифракции, 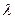 – длина волны де Бройля. – длина волны де Бройля. |
Выражая из формулы (3.27) длину волны де Бройля, получим:
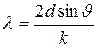 . (3.28)
. (3.28)
Воспользуемся выражением длины волны де Бройля через импульс частицы и постоянную Планка:
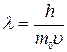 . (3.29)
. (3.29)
Из формулы (3.29) найдем скорость электрона:
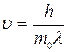 . (3.30)
. (3.30)
Вычислим искомые величины по формулам (3.29) и (3.30):
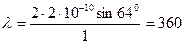 пм;
пм;
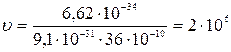 м/с = 2 Мм/с.
м/с = 2 Мм/с.
Ответы: 360 пм; 2 Мм/с.
4. Электрон в плоскопараллельном слое толщины 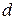 из вещества, показатель преломления которого
из вещества, показатель преломления которого 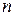 , движется со скоростью
, движется со скоростью 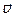 перпендикулярно ограничивающим слой плоскостям. Скорость электрона
перпендикулярно ограничивающим слой плоскостям. Скорость электрона 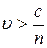 , при этом регистрируется излучение Вавилова – Черенкова. Определить угол
, при этом регистрируется излучение Вавилова – Черенкова. Определить угол 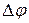 раствора конического сектора, в котором сконцентрировано излучение вследствие конечности толщины слоя.
раствора конического сектора, в котором сконцентрировано излучение вследствие конечности толщины слоя.
 Дано: Дано: 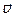 ; ; 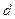 ; ; 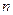 ; ; 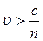 Найти: Найти: 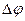 -? -? | Решение  Изобразим схематически описанную в задаче ситуацию (рисунок 3.5). Изобразим схематически описанную в задаче ситуацию (рисунок 3.5). |
Угол 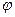 между направлением полета частиц и направлением излучения определяется из равенства
между направлением полета частиц и направлением излучения определяется из равенства
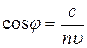 , (3.31)
, (3.31)
где 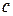 - скорость света в вакууме,
- скорость света в вакууме, 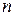 - показатель преломления среды,
- показатель преломления среды, 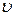 - модуль скорости частицы.
- модуль скорости частицы.
Неопределенность импульса электрона, находящегося в слое вещества толщиной d, составляет величину порядка
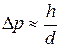 , (3.32)
, (3.32)
а неопределенность его скорости равна
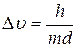 , (3.33)
, (3.33)
где 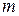 – масса электрона.
– масса электрона.
Продифференцируем левую часть выражения (3.31) по 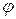 , а правую часть – по
, а правую часть – по 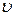 :
:
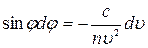 . (3.34)
. (3.34)
Считая неопределенности угла 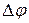 и скорости
и скорости 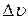 малыми величинами, представим (3.34) в виде:
малыми величинами, представим (3.34) в виде:
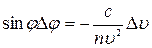 . (3.35)
. (3.35)
Из выражения (3.35) выразим модуль 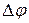 и учтем в полученном выражении формулу (3.33):
и учтем в полученном выражении формулу (3.33):
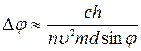 . (3.36)
. (3.36)
Числовое значение найденного угла может быть определено после задания значений показателя преломления среды, толщины слоя и скорости электрона. При этом следует определить 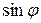 с применением основного тригонометрического тождества и формулы (3.31).
с применением основного тригонометрического тождества и формулы (3.31).
5. Комптоновское рассеяние квантов на электронах атомов осложняется тем, что электроны в атомах не находятся в покое. Оцените связанный с этим разброс в углах разлета электронов отдачи, выбиваемых из атомов водорода при рассеянии строго назад рентгеновских квантов с длиной волны 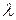 = 0,1 нм.
= 0,1 нм.
 Дано: Дано: 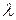 = 0,1 нм; = 0,1 нм; 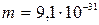 кг; кг; 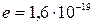 Кл Найти: Кл Найти: 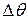 –? –? | Решение Для оценки будем считать, что начальный импульс электрона 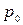 был направлен перпендикулярно направлению движения фотона. Величину был направлен перпендикулярно направлению движения фотона. Величину 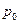 найдем из соотношения неопределенностей, записанного в виде: найдем из соотношения неопределенностей, записанного в виде: 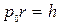 . (3.37) . (3.37) |
При этом неопределенность в положении электрона можно отождествить с радиусом первой боровской орбиты (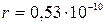 м).
м).
Продольную составляющую импульса электрона после его взаимодействия с фотоном найдем, воспользовавшись законом сохранения импульса:
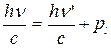 , (3.38)
, (3.38)
а изменение частоты 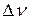 – применяя формулу Комптона
– применяя формулу Комптона
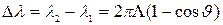 , (3.39)
, (3.39)
где 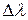 – комптоновское смещение длины волны,
– комптоновское смещение длины волны,  пм – комптоновская длина волны для электрона,
пм – комптоновская длина волны для электрона, 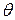 – угол рассеяния. Так как рассматривается рассеяние строго назад, то
– угол рассеяния. Так как рассматривается рассеяние строго назад, то
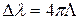 . (3.40)
. (3.40)
Определяя импульс (скорость) электрона в ходе решения системы уравнений (3.38) и (3.40), легко убедиться, что
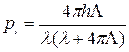 , (3.41)
, (3.41)
и что электрон в данной задаче нерелятивистский.
Оценим теперь разброс в угле рассеяния электрона (рисунок 3.6).
 |
На рисунке 3.6 видно, что
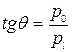 . (3.42)
. (3.42)
Учтем в (3.42) формулы (3.37) и (3.41):
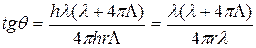 . (3.43)
. (3.43)
Тогда искомый разброс угла рассеяния определим как
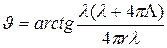 . (3.44)
. (3.44)
Производя вычисления, получим:
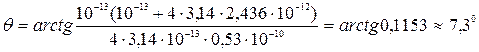 .
.
Ответ: 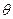 = 7,3°.
= 7,3°.
6. Оцените минимальный размер железной пылинки, при котором можно наблюдать эффект Мёссбауэра с энергией перехода Е = 14 кэВ и временем жизни 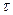 = 10-3 с, если отдачей пылинки будет обусловлено доплеровское смещение, равное естественной ширине линии.
= 10-3 с, если отдачей пылинки будет обусловлено доплеровское смещение, равное естественной ширине линии.
Примечание. Эффект Мёссбауэра заключается в том, что при достаточно низкой температуре отдачу испытывает не отдельное излучившее ядро, а весь кристалл (в рассматриваемой задаче – пылинка).
 Дано: Е = 14 кэВ; Дано: Е = 14 кэВ; 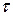 = 10-3 с; = 10-3 с; 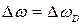 Найти: Найти: 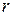 -? -? | Решение При излучении гамма-кванта пылинка приобретает импульс отдачи 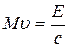 , (3.45) где Е – энергия гамма-кванта. , (3.45) где Е – энергия гамма-кванта. |
Доплеровское смещение частоты гамма-кванта вследствие движения излучателя (пылинки) определяется из соотношения
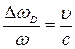 . (3.46)
. (3.46)
Естественную ширину линии найдем из соотношения неопределенностей:
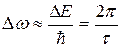 . (3.47)
. (3.47)
Комбинируя формулы (3.46) и (3.47), найдем минимальную массу пылинки, при которой еще наблюдается эффект Мёссбауэра:
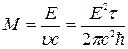 . (3.48)
. (3.48)
Оценим радиус пылинки, считая, что она имеет сферическую форму. Так как объем шара
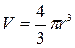 (3.49)
(3.49)
и, иначе,
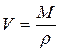 , (3.50)
, (3.50)
то, комбинируя формулы (3.48), (3.49) и (3.50), получим:
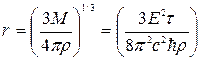 . (3.51)
. (3.51)
Вычислим по формуле (3.51) оценочное значение радиуса пылинки, приняв ее плотность равной 8000 кг/м3:
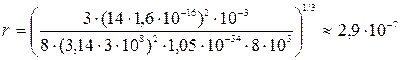 м.
м.
Ответ: 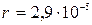 см.
см.
 2015-03-20
2015-03-20 5276
5276