Указание к выполнению

1. Для степенного ряда вида

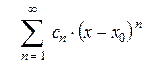
в случае, когда все коэффициенты ряда 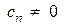(т.е. ряд содержит все целые положительные степени выражения 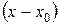), интервал сходимости определяется неравенством

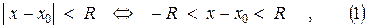
где радиус сходимости 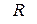определяется по формуле Даламбера (2) или по формуле Коши (3):

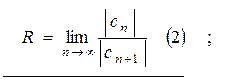
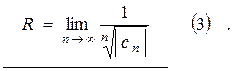
2. Если же степенной ряд содержит не все целые положительные степени выражения 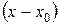(например, степенной ряд содержит члены только с четными или только с нечетными степенями выражения ),

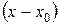то

в этом случае степенной ряд рассматривается как функциональный ряд общего вида

,

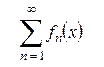интервал сходимости которого определяется с помощью признака Даламбера (4) или признака Коши (5) (применяемых к ряду ):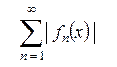

.

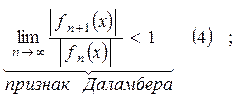
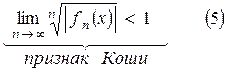3. Исследовать сходимость степенного ряда в граничных точках интервала сходимости.