2015-03-20
537
Основные расчетные предпосылки при расчете железобетонных изгибаемых элементов такие же, как и для элементов без сжатой арматуры.
Рассмотрим усилия, действующие в поперечном сечении изгибаемого элемента при учете сжатой арматуры
,
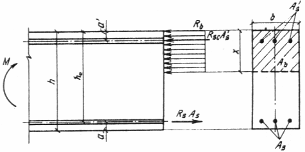
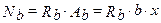Усилие в сжатой арматуре может быть определено следующим образом:
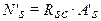
Усилие в растянутой арматуре может быть определено следующим образом:
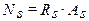
Из уравнения равновесия (равенства нулю проекции всех сил на продольную ось элемента) следует, что:
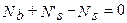, т.е.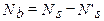 
или
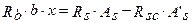
Запишем уравнение моментов всех сил относительно оси растянутой арматуры
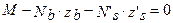
или
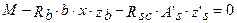
в данном случае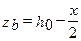 
, 
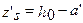
получаем
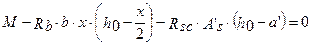
или
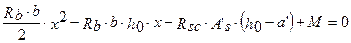
как видим из приведенного выше уравнения, разрешение его относительно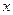 
возможно только при исключении еще одного неизвестного – 
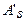, т.е. на данном этапе необходимо задаться площадью сжатой арматуры. Наиболее рационально площадь сжатой арматуры назначать таким образом, чтобы сумма площадей сжатой и растянутой арматуры была минимальной, в этом случае усилие в бетоне принимается равным предельному значению, т.е.
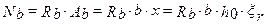
тогда
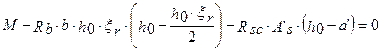
откуда
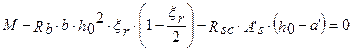
так как
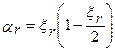, получаем
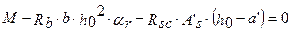, откуда
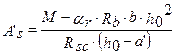, т.е. формулу 3.24 из [2].
так как 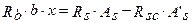и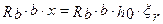 
получаем
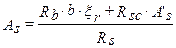
или
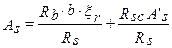
в случае если расчетное сопротивление арматуры сжатию и растяжению совпадает, т.е.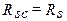 
, получаем частный случай приведенной выше формулы:
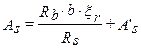, т.е. формулу 3.25 из [2].
более точно площадь растянутой арматуры можно найти следующим образом. Высоту сжатой зоны бетона найдем из уравнения
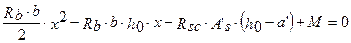
находим корни данного уравнения
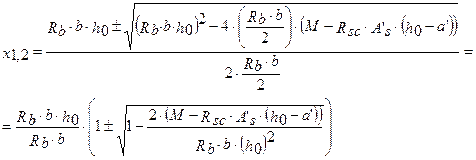
обозначив
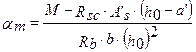- относительная величина изгибающего момента
получаем
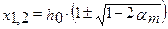
Очевидно, что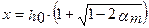 
не может являться корнем уравнения, т.к. выражение в скобках превышает 1, и высота сжатой зоны превысит рабочую высоту сечения, что не является искомым корнем. Таким образом, единственным верным корнем уравнения является:
так как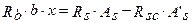
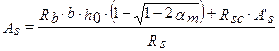
или
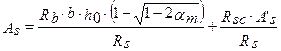
в случае, если расчетное сопротивление арматуры сжатию и растяжению совпадает, т.е. 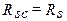, получаем частный случай приведенной выше формулы:
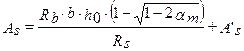, т.е. формулу 3.26 из [2].
