Решение задачи, когда на обсадную трубу совместно действует и осевая сила, и боковое давление имеет несколько вариантов.
При рассматриваемой схеме нагружения в теле возникает сложное напряженное состояние. Можно воспользоваться одной из теорий прочности, найти эквивалентное напряжение, и, приравняв его пределу текучести, решить полученное уравнение относительно предельного давления.
В наибольшей степени для этого подходит энергетическая теория прочности. Согласно этой теории моменту перехода из упругого состояния в пластическое соответствует равенство между удельной потенциальной энергии формоизменения при сложном нагружении и одноименной энергией при простом растяжении. Условие прочности при этом записывается:
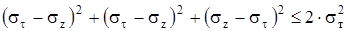 .
.
Из формулы Лямэ следует, что при 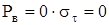 . Подставив
. Подставив 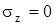 и решив его относительно
и решив его относительно 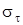 найдем наименьшее значение последнего:
найдем наименьшее значение последнего:
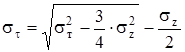 .
.
Если в эту формулу вместо 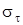 подставить его значение, полученное из формулы Лямэ, получим следующее выражение для определения предельного наружного гидравлического давления при одновременном приложении осевой силы для круглых равностенных труб:
подставить его значение, полученное из формулы Лямэ, получим следующее выражение для определения предельного наружного гидравлического давления при одновременном приложении осевой силы для круглых равностенных труб:
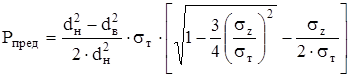 .
.
Если положить здесь 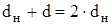 и
и 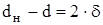 , а также
, а также 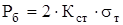 получим окончательно:
получим окончательно:
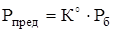 ,
,
где: 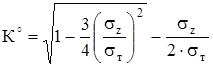 .
.
Имеется ряд аналогичных формул, это A. A. Гайворонского,
Л. Ю. Измайлова.
Т. Е. Еременко предложил эмпирическую формулу:
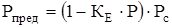 ,
,
где: 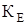 - эмпирический коэффициент, определенный автором для обсадных труб с наружным диаметром 146 и 168 мм групп прочности Д и К,
- эмпирический коэффициент, определенный автором для обсадных труб с наружным диаметром 146 и 168 мм групп прочности Д и К,
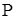 - осевая растягивающая сила.
- осевая растягивающая сила.
 2015-03-20
2015-03-20 654
654








