2015-03-20
2199
Процедура перехода от одного опорного плана к другому алгоритмически выполняется таким образом. Пусть выбран некоторый небазисный элемент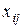 
, который вводится в базис. Отметим его знаком «+». Дальше строится замкнутая цепочка, вершинами которой будут базисные элементы опорного плана. Вершины цепочки отражаются знаком «+» и «-» по очереди, соблюдая правило: каждая строка и столбец должны иметь столько элементов, отмеченных знаком «-», сколько и «+».Среди элементов, отмеченных знаком «-» выбирается минимальный элемент. Определим его через 
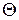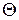. добавляется к элементам, отмеченным знаком «+», и вычитается из элементов, отмеченных знаком «-».
Оптимальность опорного плана проверяется согласно величине оценок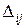 
, причем 
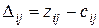. Параметры 
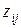вычислим, таким образом, для 
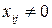имеем систему уравнений вида 
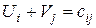. Таких уравнений есть 
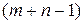, откуда можно определить компоненты Ui и Vj вектора, который вводится. Искомых величин есть 
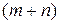, а уравнений на одно меньше. Для определенности предусматривается 
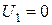, что, а другие определяются из системы уравнений. Зная значение Ui и Vj, можно определить параметры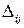 
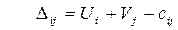
Другими словами, для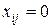 
вычисляются значения 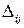. Транспортная задача является задачей минимизации. Опорный план оптимальный, если все 
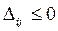. Если план неоптимален, то среди положительных 
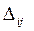выбирается максимальный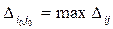 
Элемент с номером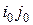 
подлежит введению в базис (он является первым элементом при построении цепочки). Метод решения задач транспортного типа называется методом потенциалов. Метод основан на идее нахождения потенциалов (величин Ui и Vj) и выборе компоненты, что вводится в базис, если опорный план неоптимальный.
Алгоритм метода потенциалов представляет пошаговый процесс, который состоит из проверки на оптимальность опорного плана, вырожденности и переход на новый опорный план. Процесс руководствуется признаком оптимальности. Опишем этот процесс.
Шаг 0. Возвести данные в таблицу и определить опорный план. Если план вырожден, то ввести нулевые базисные элементы.
Шаг 1. Составить систему уравнений для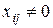 
и вычислить все потенциалы Ui и Vj.
Шаг 2. Вычислить значение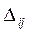 
для небазисных компонент.
Шаг 3. Если план неоптимален, то определить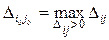 
В другом случае перейти к шагу 6.
Шаг 4. Построить цепочку, начиная с элемента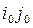 
и определить как минимальный элемент среди элементов, отмеченных знаком минус.
Шаг 5. Определить новый опорный план; если имеет место вырожденность, то ввести нулевые базисные компоненты. Перейти к шагу 1.
Шаг 6. Выписать базисные компоненты из последней таблицы и определить значение целевой функции
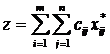
где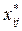 
- оптимальные значения перевозок.
Пример: Проверим оптимальность опорного плана, построенного методом северо-западного угла из предыдущей задачи.
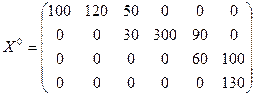
Значение целевой функции для этого плана: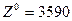 
План невырожден, т.к. в нем 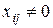- 9, и 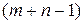= 4+6-1=9.
Составим систему уравнений для 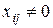и вычислим все потенциалы Ui и Vj.
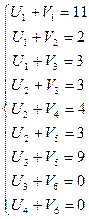
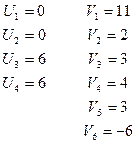
Вычислим значение для небазисных компонент.(
)
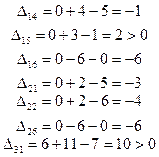
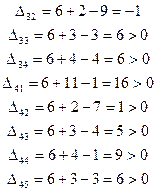
Т.к. есть 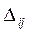положительные то план 
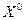не оптимален. Построим новый план.
Найдем максимальную оценку больше нуля: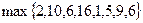 
=16. Значит вводить в план будем элемент 
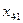. Начиная с этого элемента построим цепочку.
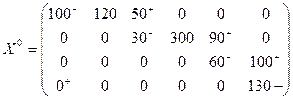
Найдем минимальный элемент в цепи, стоящий со знаком минус.
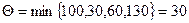. Построим план 
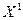учитывая знаки цепи.
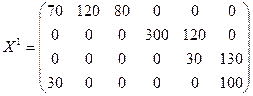
Посчитаем значение целевой функции для этого плана: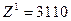 
Значение целевой функции уменьшается, значит вычисление идет верно.
Проверим полученный план 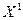на оптимальность. Для этого повторим процесс проверки как для плана 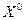. Процесс необходимо повторять до тех пор пока не получим план со всеми оценками больше или равными нулю.
Вопрос для самоподготовки
1. Суть способа перехода от одного опорного плана к другому.
2. Что определяется потенциалами в методе потенциалов?
3. Каким должны быть все в методе потенциалов, чтобы план был оптимальным?
ЛЕКЦИЯ 9.
Метод потенциалов для транспортной задачи с планом построенным
