2015-04-08
446
В рассматриваемой работе на основе теоретических моделей массового обслуживания предусмотрено проведение расчетов характеристик надежности работы ГПС, интенсивности поступления деталей на транспортер ГПС в зависимости от заданной вероятности отказа в обслуживании.
Теория массового обслуживания занимается вопросами образования очередей, обслуживанием заявок – однотипных требований, которые поступают с систему в массовом количестве. Обслуживание происходит прибором (терминология ТМО), который расположен на канале обслуживания. Приборов и соответствующих каналов обслуживания может быть несколько. Существует ряд разновидностей моделей: с неограниченной очередью, с ограничением длины очереди, с отказом в обслуживании (при занятом канале), с приоритетом и др. Поток заявок подчиняется распределению Пуассона...
Система массового обслуживания может быть описана графом состояний. Состояния системы изображаются прямоугольниками, а возможные переходы – стрелками.
Рассмотрим пример случайного процесса: техническое устройство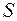 
состоит из двух узлов, каждый из которых в случайный момент времени может отказать. После чего мгновенно начинается ремонт узла, тоже продолжающийся случайное время. Возможные состояния системы:
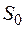- оба узла исправны
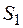- 1-й узел ремонтируется, второй исправен
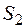- 2-й узел ремонтируется, первый исправен
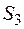- оба узла ремонтируются.
 |
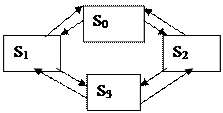Рис. 4.2. Граф состояний
В зависимости от типов моделей графы состояний системы будут различными.
Рассмотрим многоканальную систему с отказами. В качестве примера рассмотрим станочную систему, состоящую из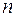 
параллельно работающих единиц оборудования и оснащенную центральным накопителем емкости на 
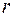мест. В накопитель поштучно поступают заготовки с интенсивностью 
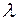. Каждая поступившая в систему заготовка доступна для обработки, если в ней имеется хотя бы один свободный станок, в противном случае заготовки ожидают своей очереди обработки в накопителе. Интенсивность обработки 
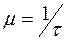, где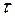 
-средняя длительность обработки. Рассматриваемая система является многокритериальной СМО с ограниченной очередью.
Рассмотрим возможные состояния системы: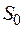 
- все станки и накопитель свободны; 
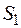- занят один станок, остальные станки и накопитель свободны; 
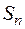- заняты все станки, накопитель свободен; 
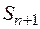- заняты все станки и одно место в накопителе; 
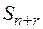- заняты все станки и все места в накопителе.
Таким образом, состояние системы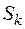 
определяется числом находящихся в ней заготовок 
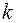(требований).
Увеличение числа занятых станков и мест в накопителе, переход из состояния 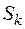в состояние 
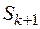происходит под действием входного потока заготовок с интенсивностью 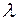. Пропускная способность одновременно работающих станков суммируется, поэтому переход из состояния 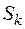в состояние 
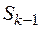определяет поток событий с интенсивностью 
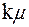, есл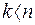и 
и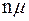 
, если 
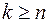. На рисунке показан граф состояний рассматриваемой системы.
Граф состояний системы изображен на рис. 4.3.
Рис. 4.3. Граф состояний системы
Обозначим через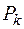 
вероятность того, что система находится в состоянии 
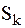. Принимая, что число уходов и приходов в каждое из возможных состояний будет сбалансированным, граф состояния можно описать следующей системой уравнений Колмогорова:
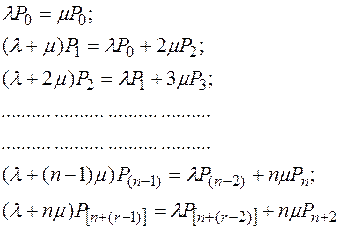
Поскольку система с достоверностью может находиться в любой из возможных 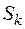состояний, то 
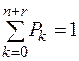. Решая систему уравнений и вводя обозначения 
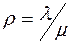, определяем вероятность того, что занято k каналов обслуживания (станков и мест в накопителе) по формуле
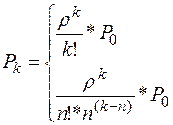
при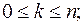 
(4.1)
при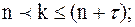 
Вероятность, что все каналы обслуживания свободны (все станки и места в накопителе свободны) определяется по формуле
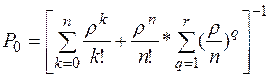(4.2)
Поступающие в систему заготовки получают отказ, если заняты все станки и накопитель, т.е. при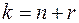 
. Вероятность отказа равна
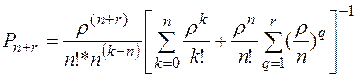(4.3)
Число станков, занятых обработкой, вытекает из состояния 
. Среднее число занятых станков в установившемся процессе обработки деталей равно
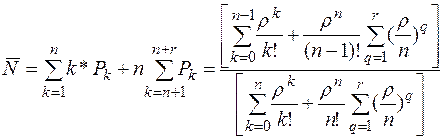
(4.4)
Если в момент поступления заготовки все станки заняты и, кроме того, уже имеется очередь в накопителе из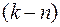 
заготовок, то средняя длительность ожидания обработки равна
.
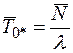Приведенная методика анализа и полученные общие зависимости могут быть использованы и для решения других частных задач. При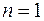 
имеет место одноканальная СМО с очередью (например, станок с локальным накопителем) при 
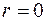будем рассматривать 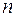- канальную систему с отказами.
