2015-04-08
2921
Как было показано выше, применение обычного МНК для оценки вектора параметров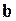 
в условиях гетероскедастичности позволяет получить несмещенные состоятельные оценки этого вектора, но стандартные ошибки полученных оценок смещены. Проблема их корректировки возникает потому, что большинство компьютерных пакетов при оценивании коэффициентов регрессии вычисляют стандартные ошибки этих коэффициентов по формуле обычного МНК, т.е. 
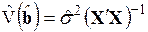, и, следовательно, эффект гетероскедастичности в них не учитывается. Рассмотрим два способа, позволяющих получить стандартные ошибки с поправкой на гетероскедастичность.
Стандартные ошибки в форме Уайта. В этой форме стандартные ошибки вычисляются тогда, когда матрица ковариаций вектора ошибок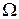 
диагональна, т.е. 
, 
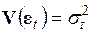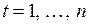. Учитывая, что оценка МНК может быть представлена в виде
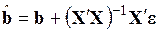, (3.80)
ковариационная матрица записывается следующим образом
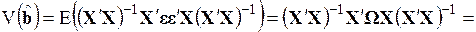
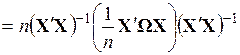. (3.81)
Распишем произведение матриц через сумму
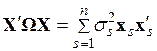, (3.82)
где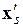 
– 
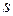-я вектор-строка матрицы регрессоров.
Уайт показал, что замена неизвестных величин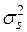 
на остатки в квадрате 
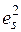позволяют получить состоятельную оценку матрицы ковариаций оценок коэффициентов регрессии в виде следующего выражения:
|
|
|
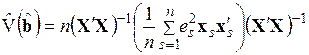. (3.83)
Рассчитанные по это формуле ошибки называются стандартными ошибками в форме Уайта.
Стандартные ошибки в форме Невье – Веста. Если ненулевые элементы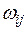 
матрицы 
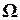стоят не только на главной диагонали, но и на соседних диагоналях, отстающих от главной не более чем на 
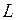(при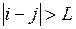 
, 
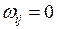), то выражение
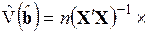
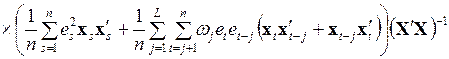, (3.84)
как показали Невье – Вест, дает состоятельную оценку матрицы ковариаций оценок коэффициентов регрессии. В формулу (3.84) включены весовые коэффициенты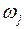 
, от выбора которых зависят стандартные ошибки. Существует несколько способов выбора этих весовых коэффициентов. Простейший случай 
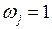следует исключить из рассмотрения, так как при таком выборе весовых коэффициентов может оказаться, что матрица (3.84) не является неотрицательно определенной. Обычно рассматривают два способа, предложенные Бартлеттом
1) 
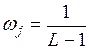; (3.85)
и Парзеном:
2) 
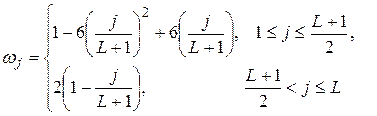. (3.86)
В большинстве случаев рекомендуется использовать весовые коэффициенты Парзена.
Рассчитанные по формуле (3.84) стандартные отклонения принято называть стандартными ошибками в форме Невье – Веста или стандартными ошибками с учетом гетероскедастичности и автокорреляции.
Тесты на гетероскедастичность
Наличие гетероскедастичности не является очевидным фактом, поэтому при построении регрессионных моделей возникает вопрос о тестировании на гетероскедастичность. Как правило, в этих тестах проверяется нуль-гипотеза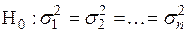 
против альтернативной гипотезы 
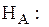предположение 
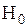не выполняется.
|
|
|
Тест Уайта. В этом тесте используется идея, состоящая в том, что наличие гетероскедастичности является следствием взаимосвязи дисперсии ошибок с регрессорами. Тест построен на проверке этой взаимосвязи без использования каких-либо предположений относительно структуры гетероскедастичности. Последовательность проверке в соответствии с тестом Уайта состоит в следующем. Сначала с помощью обычного МНК строится регрессионная модель, и находятся остатки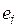 
, 
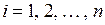. После чего строится регрессия квадратов этих остатков на все регрессоры, их квадраты и попарные произведения. В предположении, что гипотеза 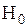имеет место, величина 
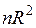асимптотически имеет распределение 
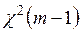, где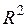 
– коэффициент детерминации, а 
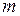– число регрессоров второй модели. Если 
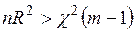, то 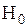отвергается. Тест универсален и может применяться в любых ситуациях. Однако, в тех случаях, когда гипотеза 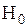отвергается, с помощью этого теста не удается установить структурную форму гетероскедастичности и, поэтому либо применяется другой тест, либо используются стандартные ошибки в форме Уайта.
Тест Голдфельда – Куандта. Тест используется в тех случаях, когда есть основания предполагать, что дисперсия ошибки зависит от некоторой независимой переменной. Краткое описание теста выглядит так:
1) данные упорядочиваются по убыванию той независимой переменной, от которой в соответствии с предположением зависит дисперсия ошибки;
2) 
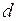наблюдений, расположенных в середине упорядоченного ряда, исключаются ( 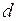рекомендуется брать равным четверти общего числа наблюдений);
3) по первым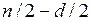 
и последним 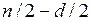строятся независимо друг от друга два регрессионных уравнения и с их помощью рассчитываются соответствующие вектора остатков 
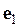и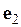 
;
4) из полученных остатков рассчитывается статистика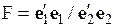 
. Если верна гипотеза 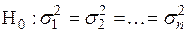, то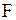 
имеет распределение Фишера с 
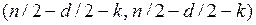степенями свободы. Если статистика больше табличного значения, то гипотеза 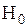отвергается.
Этот тест можно использовать в тех случаях, когда есть предположение, что дисперсия принимает два значения (двухуровневая дисперсия).
Тест Бреуша – Пагана. Тест рекомендуется применять, если априори предполагается, что дисперсия есть линейная функция от некоторых дополнительных переменных, т.е.
, 
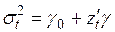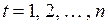, (3.87)
где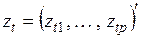 
– вектор независимых переменных;
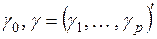– неизвестные параметры.
Проверка с помощью этого теста осуществляется так:
1) строится обычная регрессия, и с ее помощью рассчитываются компоненты вектора остатков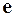 
;
2) полученные остатки используются для получения оценки дисперсии
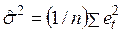; (3.88)
3) строится регрессионное уравнение
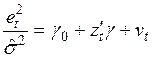, (3.89)
для которого рассчитывается объясненная часть вариации, т.е. сумма квадратов отклонений расчетных значений от среднего значения, обозначаемая обычно RSS;
4) статистика RSS/2 сравнивается с табличным значением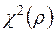 
и, если RSS/2 превосходит табличное значение, то нуль-гипотеза (отсутствие гетероскедастичности) отбрасывается. Возможность такой проверки обеспечивается результатом, установленным Бреушем и Паганом, в соответствии с которым при выполнении гипотезы 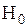величина RSS/2 асимптотически имеет распределение .
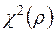В тех случаях, когда среди расчетных значений уравнения регрессии, построенного в п. 3), имеется много отрицательных, можно рекомендовать использовать вместо линейной зависимости экспоненциальную форму гетероскедастичности
, 
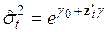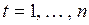. (3.90)
Использование экспоненциальной формы приводит к замене линейной регрессии п. 3) на регрессию
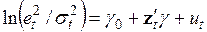. (3.91)
Рассмотренные варианты обобщенной схемы МНК обеспечивают построение моделей с коэффициентами, обладающими всеми необходимыми свойствами оценок МНК несмотря на то, что данные не отвечают требованиям однородности.
