Методические указания и задания
К контрольным работам студентов
I курса заочного отделения
(для ЗПМ)
Составители: Ваксман К.Г.
Михайлова А.В.
Москва,
2011 г.
Контрольная работа № 1а
Тема: «Пределы и непрерывность»
Основные теоретические сведения
(см. «Методические указания»)
- Символика
с – постоянная
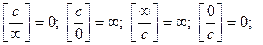
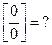 (неопределенность);
(неопределенность); 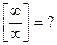 (неопределенность).
(неопределенность).
- Бесконечно-малые и бесконечно-большие функции
Функция 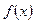 называется бесконечно-малой (бесконечно-большой) при
называется бесконечно-малой (бесконечно-большой) при 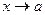 , если
, если 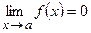 (
(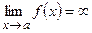 ).
).
- Предел отношения двух многочленов
1) 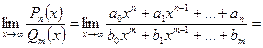
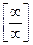 . Для раскрытия неопределенности
. Для раскрытия неопределенности 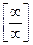 числитель и знаменатель требуется разделить на
числитель и знаменатель требуется разделить на 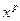 ,где
,где 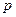 - наибольший показатель степени при
- наибольший показатель степени при 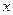 в числителе и знаменателе. Затем использовать, что
в числителе и знаменателе. Затем использовать, что 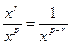 и
и 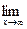
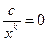 при
при 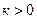 .
.
2) 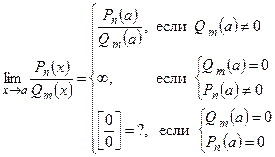
Для раскрытия неопределенности 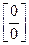 числитель и знаменатель требуется разложить на множители и сократить на общий множитель
числитель и знаменатель требуется разложить на множители и сократить на общий множитель 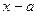 . Использовать формулы:
. Использовать формулы: 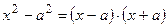 ;
;
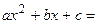
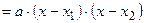 ,где
,где 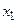 и
и 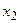 –корни,
–корни, 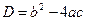 ,
, 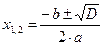 ;
;
- Первый замечательный предел
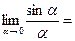
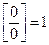 при
при 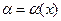 . Следствие:
. Следствие: 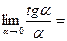
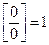 , так как
, так как 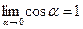 .
.
Сделав замену переменной 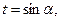 получим
получим 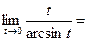
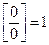 , аналогично:
, аналогично: 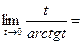
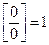 .
.
Использовать формулы: 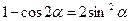 ;
; 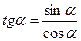 ;
; 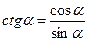 .
.
- Второй замечательный предел
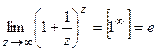 ;
; 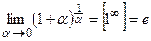 . Число
. Число 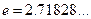
6. Функция 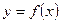 называется непрерывной в точке
называется непрерывной в точке 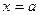 , если
, если 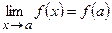 .
.
7. Условия непрерывности функции 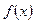 в точке
в точке 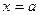 :
:
1) функция 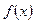 должна быть определена в некотором интервале, содержащем точку а (т.е. в самой точке и вблизи этой точки);
должна быть определена в некотором интервале, содержащем точку а (т.е. в самой точке и вблизи этой точки);
2) функция должна иметь одинаковые односторонние пределы:
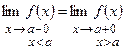 ;
;
3) эти односторонние пределы должны быть равны 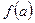 .
.
 2015-04-08
2015-04-08 402
402







