2015-04-08
3001
Пусть есть ориентированный граф G=(V, E), у которого все дуги имеют неотрицательные метки, а одна вершина определена как источник. Задача состоит в нахождении стоимости кратчайших путей от источника ко всем другим вершинам граф G. Длина пути определяется как сумма стоимостей дуг, составляющих путь. Эта задача часто называется задачей нахождения кратчайшего пути с одним источником. При этом длина пути может измеряться даже в нелинейных единицах, например во временных.
Для решения поставленной задачи будем использовать алгоритм Дейкстры. Алгоритм строит множество S вершин, для которых кратчайшие пути от источника уже известны. На каждом шаге к множеству S добавляется та из оставшихся вершин, расстояние до которой от источника меньше, чем для других оставшихся вершин. Если стоимости всех дуг неотрицательны, то кратчайший путь от источника к конкретной вершине проходит только через вершины множества S. Такой путь называют особым. На каждом шаге алгоритма используется массив D, в который записываются длины кратчайших особых путей для каждой вершины. Когда множество S будет содержать все вершины орграфа, т.е. для всех вершин будут найдены особые пути, тогда массив D будет содержать длины кратчайших путей от источника к каждой вершине. Ниже приведен фрагмент программного кода алгоритма Дейкстры. FL – массив типа Boolean. Если значение его элемента равно false, то соответствующий ему элемент массива D должен проверяться на предмет поиска кратчайшего пути, в противном случае этот элемент больше не участвует в рассмотрении.
For m:=1 to n do
P[m]:=1; {Р – массив, используемый для построение кратчайших путей}
For j:=1 to n do
D[j]:=C[i,j]; {C - матрица цен}
For j:=2 to n do
Begin
m:=2;
While fl[m]= true do m:=m+1;
w:=D[m];
s[j]:=m;
For k:=m+1 to n do
if fl[k]=false then
if D[k]< w then
begin
w:=D[k];
s[j]:=k;
end;
v:=s[j];
fl[v]:=true;
for i:=1 to n do begin
if D[i]> D[v]+C[v,i] then P[i]:=v;
D[i]:=min(D[i], D[v]+C[v,i]);
end;
end;
Здесь предполагается, что в орграфе G вершины поименованы целыми числами, т.е. множество вершин V={1, 2, … n}, причем вершина 1 является источником. Массив С – это двумерный массив стоимостей, где элемент C[i, j] равен стоимости дуги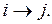 
Если дуги 
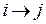не существует, то C[i, j] присваивается значение ∞, т.е. большее любой фактической стоимости дуг. На каждом шаге D[i] содержит длину текущего кратчайшего особого пути к вершине i.
Применим алгоритм Дейкстры для ориентированного графа, показанного на рис. 7.4. Вначале S={1}, D[2]=10, D[3]=∞, D[4]=30, D[5]=100. На первом шаге цикла w =2, т.е. вершина 2 имеет минимальное значение в массиве D. Затем вычисляется D[3]=min(∞, 10+50)=60. D[4] и D[5] не изменяются, т.к. не существует дуг, исходящих из вершины 2 и ведущих к вершинам 4 и 5. Последовательность значений элементов массива D после каждой итерации цикла показаны в таблице ниже.
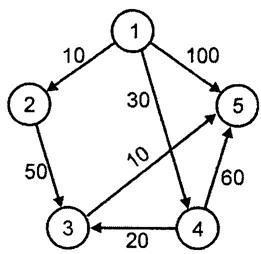
Рис. 7.4 – Помеченный орграф, к которому применен алгоритм Дейкстры
Вычисления для орграфа, изображенного на рис. 4.
В рассмотренный алгоритм можно внести изменения, которые позволят определить кратчайший путь для любой вершины графа. Для этого нужно ввести еще один массив P, где P[v] содержит вершину, непосредственно предшествующую вершине v в кратчайшем пути. Вначале P[v]= 1 для всех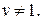 
В листинге алгоритма Дейкстры при выполнении условного оператора D[v]+C[v,i]<D[i], элементу P[i] присваивается значение v. После выполнения алгоритма кратчайший путь к каждой вершине можно найти с помощью обратного прохождения по предшествующим вершинам массива Р.
Для рассмотренного орграфа массив Р имеет следующие значения: P[2]=1, P[3]=4, P[4]=1, P[5]=3. Для определения кратчайшего пути, например от вершины 1 к вершине 5, надо отследить в обратном порядке предшествующие вершины, начиная с вершины 5. Таким образом, кратчайший путь из вершины 1 в вершину 5 составляет последовательность вершин: 1, 4, 3, 5.
