Нахождение кратчайших путей между парами вершин

Пусть дан орграф G=(V, E) и необходимо определить кратчайшие пути между всеми парами вершин орграфа. Каждой дуге 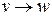этого графа сопоставлена неотрицательная стоимость C[v, w]. Общая задача нахождения кратчайших путей заключается в нахождении для каждой упорядоченной пары вершин (v, w) любого пути от вершины v в вершины w, длина которого минимальна среди всех возможных путей от v к w.

Для решения поставленной задачи применим алгоритм Флойда. Для этого пронумерует вершины графа последовательно от 1 до n.

Алгоритм Флойда использует матрицу А размера 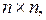в которой вычисляются длины кратчайших путей. Вначале А[i, j] = C[i, j] для всех i ≠ j. Если дуга 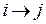отсутствует, то C[i, j]=∞. Каждый диагональный элемент матрицы А равен 0.

Над матрицей А выполняется n итераций. После к -ой итерации А[i, j] содержит значение наименьшей длины путей из вершины i в вершину j, которые не проходят через вершины с номером, большим к,т.е. между концевыми вершинами пути из i в j могут находиться только вершины, номера которых меньше или равны к. На к -ой итерации для вычисления матрицы А применяется следующая формула:

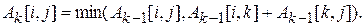
Нижний индекс к обозначает значение матрицы А после к -ой итерации. Графическая интерпретация приведенной формулы показана на рис. 7.5.

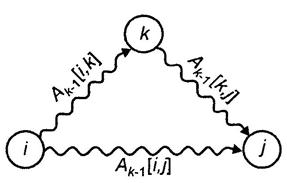
Рис. 7.5 – Включение вершины к в путь от вершины i к вершине j

Для вычисления 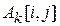проводится сравнение величины 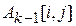с величиной 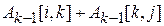. Если путь через вершину к дешевле, чем 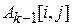, то величина 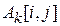изменяется.

На рис. 7.6 приведен помеченный орграф, а на рис. 7.7 – значения матрицы А после трех итераций.

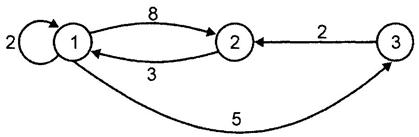
Рис. 7.6 – Помеченный орграф

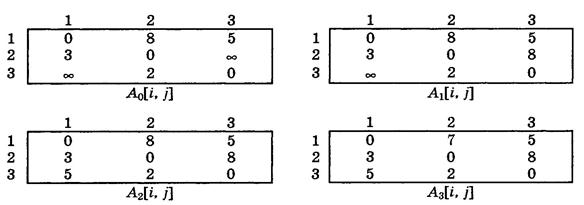
Рис. 7.7 – Последовательные значения матрицы А

Равенства 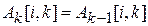и 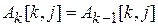означает, что на к -ой итерации элементы матрицы А, стоящие в к -ой строке и к -ом столбце, не изменяются. Процедура, реализующая алгоритм Флойда, представлена ниже.

For i:=1 to n do

For j:=1 to n do

readln(C[i,j]);

For i:=1 to n do

For j:=1 to n do

A[i,j]:=C[i,j];

For i:=1 to n do

A[i,i]:=0;

For k:=1 to n do

For i:=1 to n do

For j:=1 to n do

if A[i,k]+ A[k,j]< A[i,j] then

A[i,j]:= A[i,k]+ A[k,j];

End.

Время выполнения этой программы имеет порядок 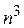. Поскольку алгоритм Дейкстры с использованием матрицы смежности находит кратчайшие пути от одной вершины за время порядка 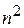, то в случае применения алгоритма Дейкстры для нахождения всех кратчайших путей потребует времени порядка 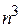, т.е. получается такой же временной порядок, как и в алгоритме Флойда. Если e, количество дуг в орграфе, значительно меньше, чем 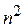, то рекомендуют применять алгоритм Дейкстры со списками смежности. Тогда время нахождения кратчайших путей имеет порядок 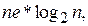что значительно луче алгоритма Флойда, хотя бы для больших разреженных графов.