
П1.2. Лабораторная работа №1 задание 2. Создание и форматирование таблиц
Варианты заданий 1–10.
1)
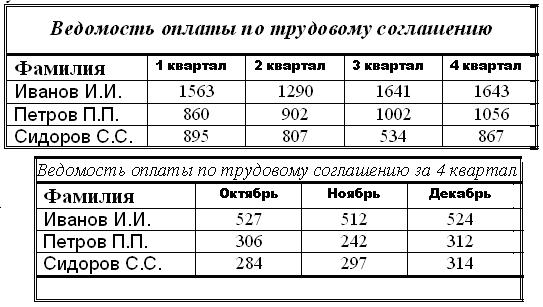
2)
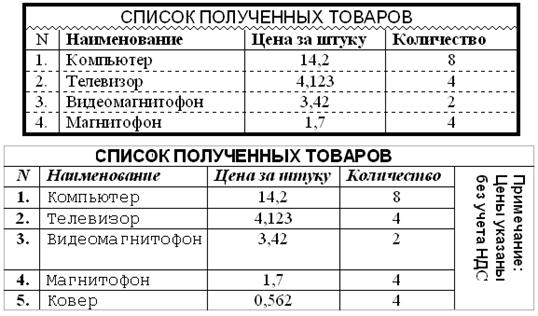
3)
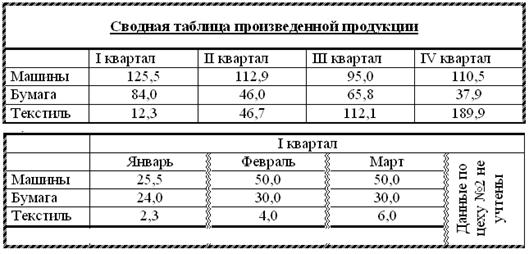
4)
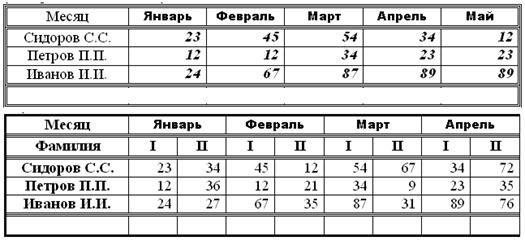
5)
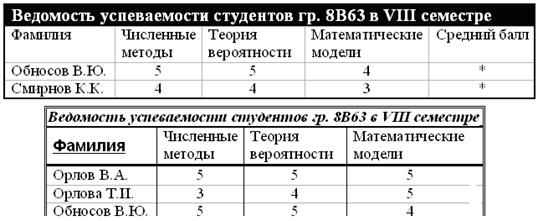
6)
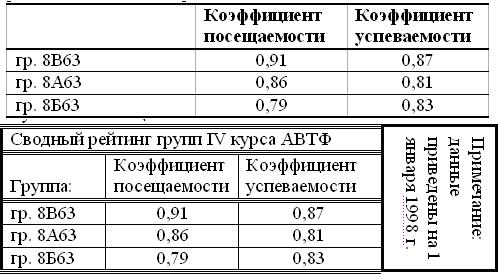
7)
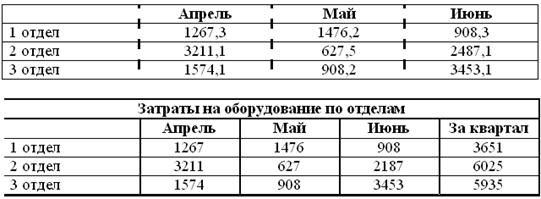
8)
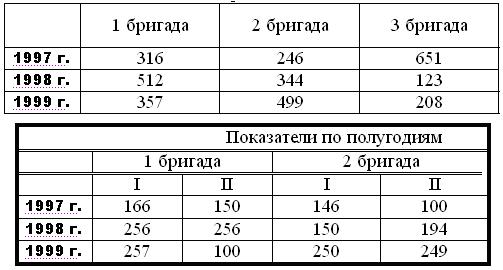
9)
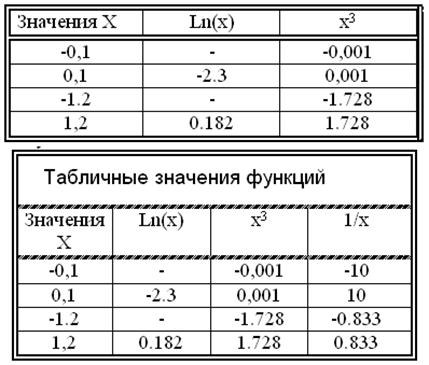
10)
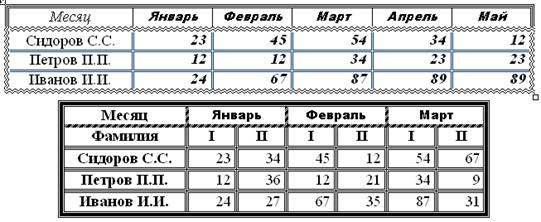
П1.3. Лабораторная работа №1 задание 3. Работа с редактором формул
Варианты заданий 1–20.
1. Векторное произведение векторов a и b в координатной форме можно записать в виде определителя 3-го порядка:
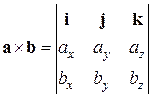 .
.
2. Объем треугольной пирамиды ABCD равен одной шестой модуля смешанного произведения векторов 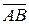 ,
, 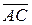 и
и 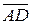 . В координатной форме это выражение запишется в виде
. В координатной форме это выражение запишется в виде
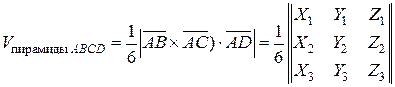 .
.
3. Вычислить выражение
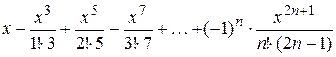 .
.
4. Производная дроби равна производной числителя, умноженной на знаменатель, минус производная знаменателя, умноженная на числитель, и все это деленное на квадрат знаменателя:
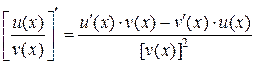 .
.
5. Элементы x и y вычисляются по формулам:
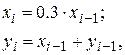
при 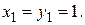 Вычислить
Вычислить 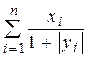 .
.
6. Вычислить выражение 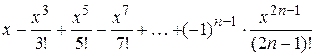 .
.
7. Найдите пределы указанных функций
а) 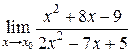 ,
, 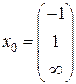 ; б)
; б) 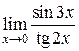 ; в)
; в) 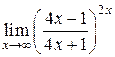 .
.
8. Значения членов числовой последовательности ai, bi вычисляются по формулам:
|
|
|
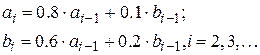
Не применяя массивов, вычислить 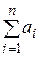 при а1 = b1 = 1.
при а1 = b1 = 1.
9. Дано действительное b<0. Последовательность 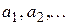 образуется по следующим формулам:
образуется по следующим формулам:
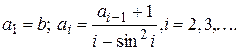
Не используя массивов, найти значение и номер первого неотрицательного члена последовательности.
10. Вычислить интеграл методом трапеций с точностью 0.0001
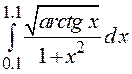 .
.
11. Вычислить 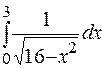 методом Симпсона с точностью 0.0001.
методом Симпсона с точностью 0.0001.
12. Вычислить 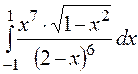 методом Симпсона с точностью 0.0001.
методом Симпсона с точностью 0.0001.
13. Вычислить 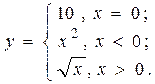
14. Вычислить 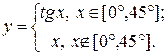
15. Вычислить 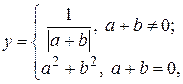 не используя функцию abs(x).
не используя функцию abs(x).
16. Вычислить значение определителя 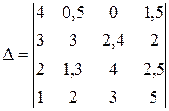
17. Найти решение системы линейных алгебраических уравнений методом Гаусса, если коэффициенты системы заданы матрицей

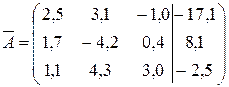 .
.
18. Найти решение системы линейных алгебраических уравнений
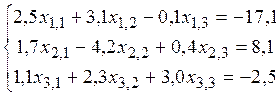 .
.
19. Найти решение системы линейных алгебраических уравнений
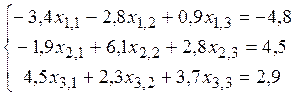 .
.
20. Найти решение системы линейных алгебраических уравнений
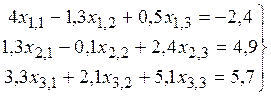 .
.
 2015-04-12
2015-04-12 475
475








