Пример 3.3 [4].Имеются выборки, содержащие стоимость 1 м2 внутренней площади объектов недвижимости в городе  за 1998-2000 г.г. Выполнить дисперсионный анализ с целью проверки однородности выборок.
за 1998-2000 г.г. Выполнить дисперсионный анализ с целью проверки однородности выборок.
Исходные данные и результаты дисперсионного анализа в среде ЭТ, показывающие возможность объединения более двух выборок разного размера, приведены в таблице 4.4.
Т а б л и ц а 4.4
Дисперсионный анализ в среде ЭТ
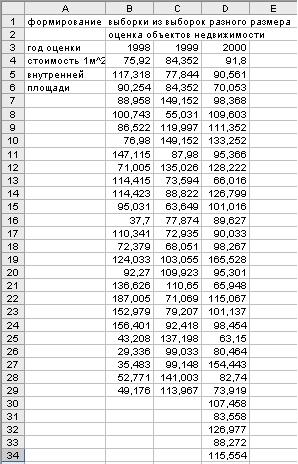
Продолжение таблицы 4.4
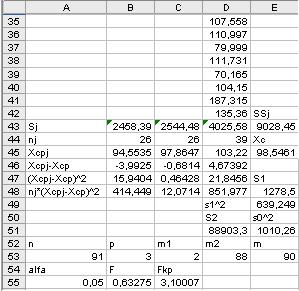
Продолжение таблицы 4.4
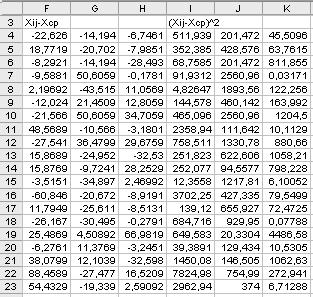
Продолжение таблицы 4.4
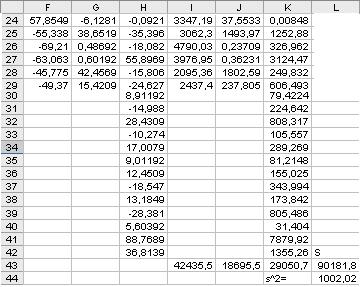
Для подтверждения этого дополнительно рассмотрим возможность объединения выборок, полученных в результате парных наблюдений. Выполним дисперсионный анализ выборок за 1998 и 1999 годы. Они имеют одинаковый размер – 26 наблюдений. Сводка дисперсионного анализа представлена в таблице 4.5.
Т а б л и ц а 4.5
Дисперсионный анализ однородности парных наблюдений
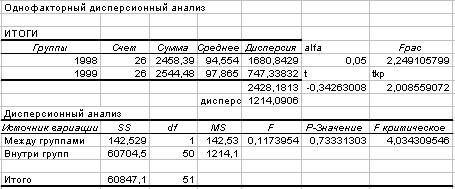
Так как 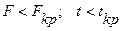 , то выборки за 1998 и 1999 годы однородны.
, то выборки за 1998 и 1999 годы однородны.
Затем покажем возможность объединения выборок разного размера – выборки за 1999 и 2000 годы. Результаты анализа приведены в таблице 4.6.
Т а б л и ц а 4.6
Дисперсионный анализ однородности выборок разного размера
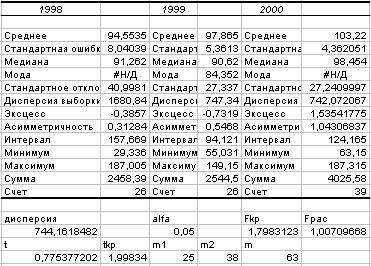
Результаты статистической обработки выборок показывают, что стоимость 1 м2 внутренней площади объектов недвижимости подчиняется нормальному закону распределения, так как среднее значение, мода и медиана имеют один порядок, а значения эксцесса и асимметричности близки к нулю.
В результате дисперсионного анализа однородности выборок за 1999 и 2000 годы установлено, что 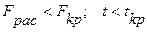 . Следовательно, эти выборки однородны.
. Следовательно, эти выборки однородны.
Таким образом, можно рассматривать возможность объединения в одну выборку более двух выборок разного размера.
Анализ дисперсионного анализа, проведенного в таблице 4.4, показывает, что для трех выборок 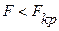 .
.
 2015-04-12
2015-04-12 546
546







