2015-04-01
670
Если твердое тело совершает крутильные колебания, то к нему может быть применен основной закон динамики вращательного движения:
,
где M – вращательный момент силы относительно оси вращения; I – момент инерции тела относительно той же оси вращения;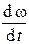 
– угловое ускорение.
Вращательный момент равен M = G кр×j. Уравнение основного закона динамики вращательного движения примет вид:
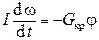, (1)
где G кр – модуль кручения2.
Из уравнения (1) видно, что в рассматриваемом движении угловое ускорение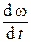 
пропорционально смещению j и направлено противоположно ему, а это есть существенный признак гармонического колебательного движения. Период колебаний можно найти, зная, что коэффициент пропорциональности между 
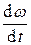и j, в данном случае 
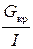, должен быть равен 
, т.е.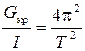 
, откуда: 
,
где Т – период крутильных колебаний прибора.
 |
Измерения и обработка результатов
Искомый момент инерции исследуемого тела в данной работе подсчитывается по формуле:
где: m и R – соответственно масса и радиус диска (эталона),
Т = t / n – период колебаний прибора с исследуемым телом (гирей),
Т 1 = t1 / n – период колебаний прибора с эталоном (диском),
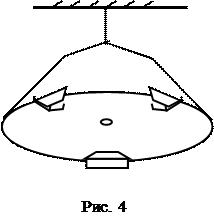
Т пр = tпр /n – период колебаний ненагруженного прибора (рис.4).
