Позиционные задачи, это те в которых определяется взаимное положение, например, определить взаимное положение прямой и плоскости, плоскости и поверхности, двух плоскостей, все это позиционные задачи.
К метрическим относятся задачи, связанные с определением истинных (натуральных) величин расстояний, углов и плоских фигур на комплексном чертеже. Можно выделить три группы метрических задач
1. Группа задач, включающих в себя определение расстояний от точки до другой точки; от точки до прямой; от точки до плоскости; от точки до поверхности; от прямой до другой прямой; от прямой до плоскости; от плоскости до плоскости. Причем расстояние от прямой до плоскости и между плоскостями измеряется в тех случаях, когда они параллельны.
2. Группа задач, включающая определение углов между пересекающимися или скрещивающимися прямыми, между прямой и плоскостью, между плоскостями (имеется в виду определение величины двухгранного угла).
3. Группа задач, связанная с определением истинной величины плоской фигуры и части поверхности (развертки).
Приведенные задачи могут быть решены с применением различных способов преобразования чертежа. В основе решения метрических задач лежит свойство прямоугольного проецирования, заключающееся в том, что любая геометрическая фигура на плоскость проекций проецируется в натуральную величину, если она лежит в плоскости, параллельной этой плоскости проекций. Решение задач значительно упрощается, если хотя бы одна из геометрических фигур, участвующих в задачах, занимает частное положение. Если одна из геометрических фигур не занимает частного положения, необходимо выполнить определенные построения, позволяющие провести одну из них в это положение.
Вопрос 6.
1. Проекция точки есть точка (рис. 1.9).
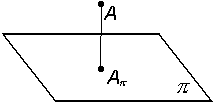
Рис. 1.9
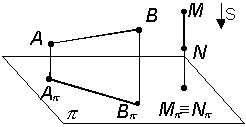
2. Проекция прямой в общем случае есть прямая (рис. 1.10).
Если прямая располагается перпендикулярно какой-либо плоскости проекций (такая прямая называется проецирующей), то на эту плоскость она проецируется в виде точки (рис. 1.10).
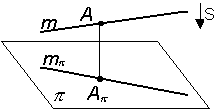
3. Если точка лежит на прямой, то ее проекция располагается на соответствующей проекции этой же прямой А 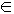 m
m 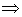 А
А 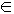 m (рис. 1.11).
m (рис. 1.11).
 |  |
| Рис. 1.10 | Рис. 1.11 |
Примечание. Первые 3 свойства проекций являются общими для центрального и параллельного проецирования.
4. Если точка делит отрезок прямой в каком-либо отношении, то ее проекция делит проекцию отрезка в том же самом отношении (рис. 1.12).
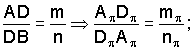
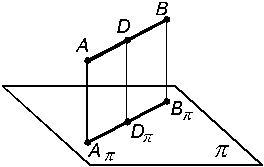
Рис. 1.12
5. Если прямая параллельна плоскости проекций, то на эту плоскость эта прямая проецируется без искажений (рис.1.13).
m II 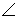
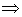 mp = m, m II p
mp = m, m II p 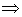 [ Аp Вp ] = [ AB ].
[ Аp Вp ] = [ AB ].
Если плоская фигура параллельна плоскости проекций, то на эту плоскость она проецируется без искажения.
6. Если прямые в пространстве пересекаются, то их проекции также пересекаются (рис. 1.14).
m  n = C
n = C 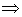 mp
mp  пp
пp 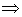 сp
сp
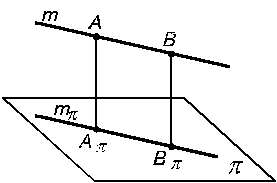 | 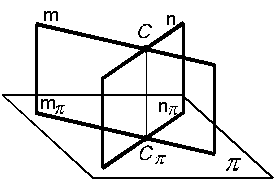 |
| Рис. 1.13 | Рис. 1.14 |
7. Если прямые в пространстве параллельны, то их проекции также параллельны (рис. 1.15).
a II b 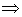 аp II b p
аp II b p
Примечание. Общими для косоугольного и прямоугольного проецирования являются свойства 4, 5, 6.
8. Если одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость прямой угол проецируется без искажений (рис. 1.16).
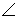 ABC = 90°; AB|| p; BC|| p;
ABC = 90°; AB|| p; BC|| p; 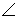 Аp Вp Сp = 90°;
Аp Вp Сp = 90°;
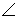 ABD = 90°; AB|| p; BD
ABD = 90°; AB|| p; BD 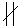 p;
p;  Аp Вp Dp = 90°.
Аp Вp Dp = 90°.
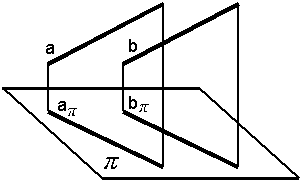 | 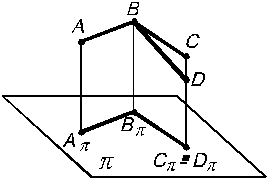 |
| Рис. 1.15 | Рис. 1.16 |
Примечание. Свойство 8-е только для ортогонального проецирования.
9. Параллельный перенос фигуры в пространстве или плоскости проекций не изменяет вида и размеров проекции фигуры.
преимущества:
а) простоту графических построений для определения ортогональных проекций точек;
б) возможность при определенных условиях сохранить на проекциях форму и размеры проецируемой фигуры.
Указанные преимущества обеспечили широкое применение ортогонального проецирования в технике, в частности для составления машиностроительных чертежей.
Сущность метода ортогонального проецирования. Его приемущества.
Как уже было сказано выше ортогональное проецирование — это частный случай параллельного проецирования. При ортогональном проецировании проецирующие лучи перпендикулярны к плоскости проекций.
Свойства ортогонального проецирования:
Все свойства параллельного проецирования выполнимы и для ортогонального проецирования. Однако ортогональные проекции обладают ещё некоторыми свойствами.
Теорема.
Если одна из сторон прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то угол на эту плоскость проецируется в виде прямого угла.
Ортогональное проецирование обеспечивает простоту геометрических построений при определении ортогональных проекций точек, а так же возможность сохранять на проекциях форму и размеры проецируемой фигуры. Эти достоинства обеспечили ортогональному проецированию широкое применение в техническом черчении.
Рассмотренные методы проецирования позволяют решить прямую задачу начертательной геометрии, т. е. по оригиналу построить плоский чертёж. Однако, полученные таким образом проекции на одну плоскость, дают неполное представление о предмете, его форме и положении в пространстве, т. е. такой чертёж не обладает свойством обратимости.
Чтобы получить обратимый чертеж, т.е. чертеж, дающий полное представление о форме, размерах и положении оригинала в пространстве, однокартинный чертеж дополняют. В зависимости от дополнения существуют различные виды обратимых чертежей.
 2015-04-12
2015-04-12 1331
1331
