2015-04-12
273
1. Определение опорной реактивной силы
Уравнение равновесия сил, направленных по оси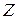 
, имеет вид
,
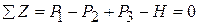откуда
.
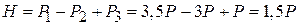2. Определение внутренних нормальных сил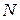 
методом сечений
и построение эпюры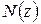 
Стержень имеет три участка, границами которых служат сечения, где приложены внешние силы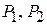 
. Для обнаружения нормальных сил на этих участках используем метод сечений. Мысленно рассекаем стержень на каждом из участков на расстояниях 
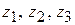и рассматриваем равновесие одной из частей рассеченного стержня, заменяя действие отброшенных частей внутренними нормальными силами 
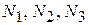(рис. 2.2 б). В результате получаем уравнения равновесия
.
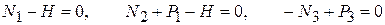С учетом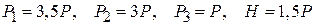 
находим
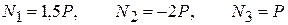. (1)
Нормальные силы (1) на каждом из участков известны, что позволяет легко построить график-эпюру нормальных сил (рис. 2.2 в).
Из эпюры находим опасное сечение или участок, где нормальные силы максимальны. Таким оказывается второй участок, на котором
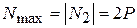. (2)
3. Расчет на прочность
Для опасных сечений второгоучастка с учетом (2) составляем условие прочности
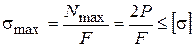. (3)
Различают три типа расчета на прочность.
Проверочный расчет на прочность
Известны все величины в условии прочности (3). Пусть, например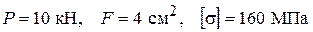 
.
Подставляя эти значения в (3), получаем:
,
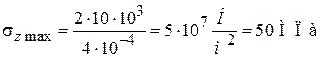что меньше допускаемого значения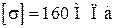 
. Следовательно, стержень удовлетворяет условию прочности.
Проектировочный расчет на прочность
Требуется найти диаметр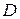 
круглого поперечного сечения стержня, для которого площадь сечения определяется формулой 
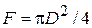. Условие (3) записывается в виде:
,
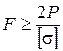тогда
.
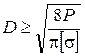Сохраняя значения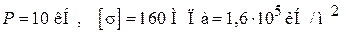 
, получаем
.
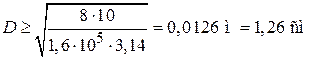Округляя, принимаем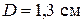 
.
Расчетное напряжение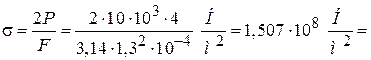 
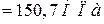, что меньше допускаемого на 5,8 %.
Определение допускаемой нагрузки
Из (3) имеем:
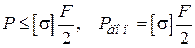. (4)
Пусть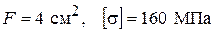 
, тогда
.
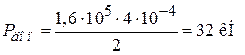4. Построение эпюры перемещений
Поскольку в задаче мы имеем три участка с различными значениями нормальных сил, то формулу (2.4) удобно записать в виде
,
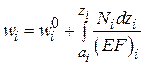где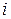 
– номер участка; 
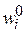– постоянная в начале i -го участка; 
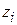– текущая координата сечения i -го участка; 
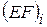– жесткость i -го участка, 
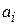– координаты начального сечения i -го участка.
На первом участке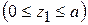 
имеем
.
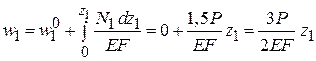Следовательно, эпюра − прямая линия.
При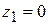 
имеем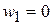 
, т. е. 
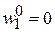при жестком защемлении.
При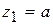 
получаем
.
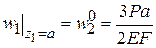На втором участке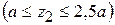 
имеем
.
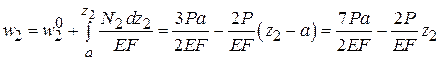Эпюра на втором участке − прямая линия.
При 
получаем
.
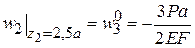На третьем участке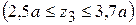 
имеем
.
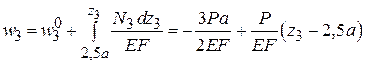При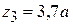 
получаем
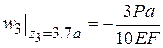. (5)
Используя полученные данные, строим график-эпюру перемещений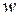 
поперечных сечений (рис. 2.2 г).
5. Расчеты на жесткость
Согласно (5), полное удлинение стержня не должно превышать условия жесткости стержня:
.
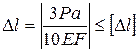Отсюда можно найти другое допускаемое значение силы:
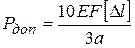. (6)
Сравнивая (4) и (6), устанавливаем из двух значений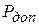 
наименьшее.
№2. Построить эпюры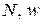 
для стержня, изображенного на рис. 2.3, при нагружении силой 
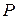и равномерно распределенной нагрузкой 
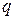. Составить условие прочности.
