2015-04-12
310
Для обнаружения внутренних сил в стержне при растяжении-сжатии применяется метод плоских сечений. Пусть стержень растягивается силой Р и собственным весом интенсивности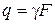 
, где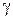 
− удельный вес материала, 
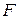− площадь поперечного сечения. Мысленно рассечем стержень на расстоянии 
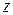от начала отсчета на верхнем его конце (рис. 2.1).
Рис. 2.1
Действие отброшенной верхней части на нижнюю заменим внутренней силой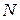 
, такой, чтобы отсеченная часть стержня находилась в равновесии. Внутреннюю силу назовем нормальной, т.к. она направлена по внешней нормали к поперечному сечению.
Уравнение равновесия имеет вид
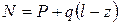. (2.1)
Дифференцируя (2.1), получаем соотношение Д. Журавского, часто используемое для контроля правильности построенного графика-эпюры 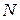методом сечений:
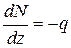. (2.2)
Если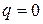 
, то из (2.2) следует, что на незагруженном участке стержня 
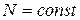, а при 
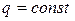на равномерно загруженном участке 
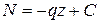, где 
− постоянная интегрирования. В этом случае 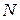− прямая линия с угловым коэффициентом 
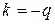. В сечении, где действует сосредоточенная сила, имеет место скачок на величину этой силы.
Если отнести силу 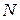к площади поперечного сечения 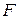, то получим силу, отнесенную к единице площади. Эту величину называют нормальным напряжением:
.
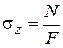Максимальное нормальное напряжение в стержне должно быть меньше некоторого безопасного значения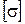 
, называемого допускаемым напряжением, т.е.
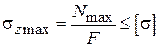. (2.3)
Условие (2.3) носит название условия прочности при растяжении-сжатии стержня. Максимальная нормальная сила определяется из графика-эпюры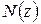 
, который строится на основании соотношения (2.1).
Под действием внешних сил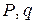 
и температуры 
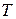стержень изменяет длину на величину
,
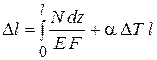где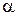 
− коэффициент линейного расширения материала; 
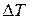− изменение температуры; 
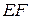− жесткость стержня при растяжении; 
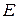− модуль упругости Эйлера – Юнга.
Если 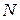− постоянная величина, то
.
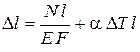Перемещение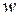 
произвольного сечения определяется по формуле
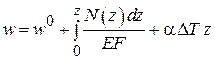, (2.4)
где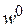 
− перемещение сечения в начале координат.
Для нашего примера при использовании (2.4) получаем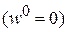 
,
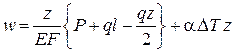т.е. график – квадратичная парабола (рис.2.1).
При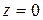 
перемещение 
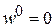, т.к. сечение жестко защемлено.
Дифференцируя (2.4) два раза получаем
.
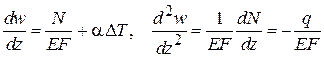По знаку второй производной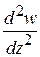 
можно определить, в какую сторону направлена выпуклость или вогнутость кривой 
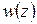. Если 
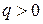, то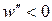 
и выпуклость кривой обращена в положительном направлении оси 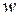, что и имеет место в нашем случае. Если 
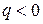, то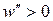 
и кривая 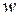будет вогнутой. Если 
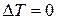, то обращение в нуль нормальной силы на графике-эпюре 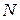является признаком экстремума на графике перемещений.
Иногда требуется ограничить удлинения либо перемещения стержней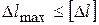 
, 
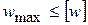, где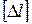 
, 
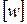− допускаемые значения удлинений и перемещений соответственно. Расчеты такого типа называются расчетами на жесткость.
