6.1. Плоскость α, проходящая через точки М 1(3;0;1), М 2(-1;2;0), М 3(0;0;-1), имеет уравнение:
А) 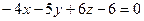 ; Б)
; Б) 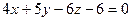 ; В)
; В) 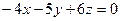 ; Г)
; Г) 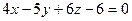
6.2. Даны координаты вершин пирамиды: А 1(4;2;5), А 2(0;7;2), А 3(0;2;7), А 4(1;5;0). Высота пирамиды 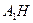 имеет канонические уравнения:
имеет канонические уравнения:
А) 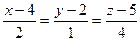 ; Б)
; Б) 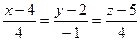 ; В)
; В) 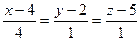 ; Г)
; Г) 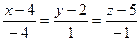 .
.
6.3. Прямая l, проходящая через точку А (-1;5;2) перпендикулярно плоскости 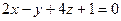 , имеет канонические уравнения:
, имеет канонические уравнения:
А) 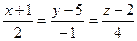 ; Б)
; Б) 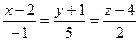 ; В)
; В) 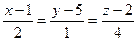 ; Г)
; Г) 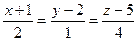 ;
;
6.4. Даны координаты вершин пирамиды: А (1;2;0), В (3;0;-3); С (5;2;6); Д (0;0;0).
Косинус угла между гранями АВС и АДС равен:
А) 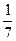 ; Б)
; Б) 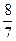 ; В)
; В) 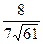 ; Г)
; Г) 
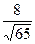 .
.
6.5. Даны координаты вершин пирамиды: А (1;2;0), В (3;0;-3); С (5;2;6); Д (0;0;0).
Синус угла между гранью АВС и ребром АД равен:
А) 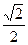 ; Б)
; Б) 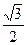 ; В)
; В) 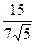 ; Г)
; Г) 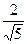 .
.
6.6. Даны координаты вершин пирамиды: А (0; 6; 4), В (3; 5; 3); С (-2; 11; -5); Д (1;-1;4). Длина высоты, проведенной из вершины А к грани ВСД, равна:
А) 6; Б) 4; В) 3; Г) 2.
6.7. Прямая l проходит через точку А (-1;3;4) перпендикулярно к плоскости 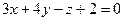 . Канонические уравнения прямой l:
. Канонические уравнения прямой l:
А) 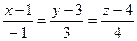 ; Б)
; Б) 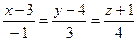 ; В)
; В) 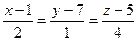 ; Г)
; Г) 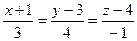 .
.
6.8. Если прямые 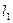 и
и 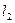 заданы уравнениями:
заданы уравнениями: 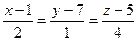 ,
, 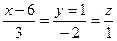 ,то:
,то:
А) 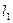 и
и 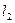 параллельны; Б)
параллельны; Б) 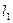 и
и 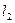 пересекаются; В)
пересекаются; В) 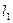 и
и 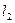 скрещиваются; Г)
скрещиваются; Г) 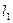 и
и 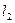 совпадают.
совпадают.
6.9. Если прямые 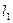 и
и 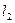 заданы уравнениями:
заданы уравнениями: 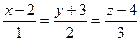 ,
, 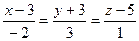 , то:
, то:
А) 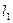 и
и 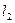 параллельны; Б)
параллельны; Б) 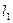 и
и 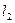 пересекаются; В)
пересекаются; В) 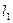 и
и 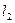 скрещиваются; Г)
скрещиваются; Г) 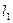 и
и 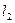 совпадают.
совпадают.
6.10. Прямая l, проходящая через точку А (1;2;1) перпендикулярно к плоскости 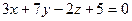 , имеет канонические уравнения:
, имеет канонические уравнения:
А) 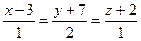 ; Б)
; Б) 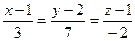 ; В)
; В) 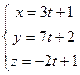 ; Г)
; Г) 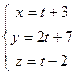 .
.
6.11. Проекция точки А (2;11;-5) на плоскость 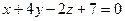 имеет координаты:
имеет координаты:
А) (-1;-1;-1); Б) (-7;0 0); В) (3;1;0); Г) (-1;-2;-1).
6.12. Плоскость α, проходящая через точку А (-1;5;8) перпендикулярно к прямой 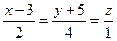 , имеет общее уравнение:
, имеет общее уравнение:
А) 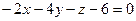 ; Б)
; Б) 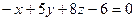 ; В)
; В) 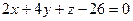 ; Г)
; Г) 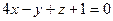 .
.
6.13. Плоскость α, проходящая через точку А (1;-2;3) и параллельная плоскости, проходящей через точки М 1(1;1;1), М 2(3;4;5), М 3(2;0;-1), имеет общее уравнение:
А) 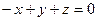 ; Б)
; Б) 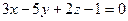 ; В)
; В) 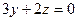 ; Г)
; Г) 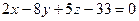 .
.
6.14. Плоскость α, проходящая через точку А (1;-2;3) и параллельная векторам 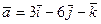 и
и 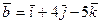 , имеет общее уравнение:
, имеет общее уравнение:
А) 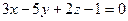 ; Б)
; Б) 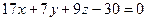 ;В)
;В) 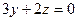 ; Г)
; Г) 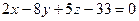 .
.
6.15. Плоскость α, проходящая через точку А (3;0;-1) и параллельная векторам
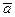 (-1;0;-4) и
(-1;0;-4) и 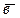 (0;1;-1), имеет общее уравнение:
(0;1;-1), имеет общее уравнение:
А) 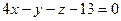 ; Б)
; Б) 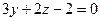 ; В)
; В) 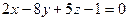 ; Г)
; Г) 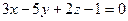 .
.
6.16. Канонические уравнения прямой 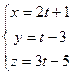 имеют вид:
имеют вид:
А) 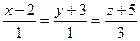 ; Б)
; Б) 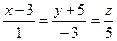 ; В)
; В) 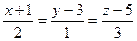 ; Г)
; Г) 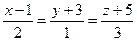 .
.
6.17. Плоскость α, проходящая через точку А (3;0;-1) и параллельная векторам 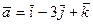 и
и 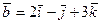 , имеет общее уравнение:
, имеет общее уравнение:
А) 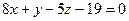 ; Б)
; Б) 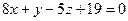 ; В)
; В) 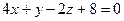 ; Г)
; Г) 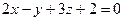 .
.
6.18. Даны координаты вершин треугольника: А (-1;2;3), В (3;1;2); С (1;3;2). Медиана АМ имеет параметрические уравнения:
А) 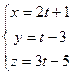 ; Б)
; Б) 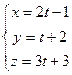 ; В)
; В) 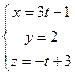 ; Г)
; Г) 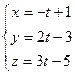 .
.
6.19. Плоскость α, проходящая через точку М (2;-1;5) перпендикулярно к плоскостям 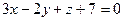 и
и 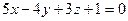 , имеет общее уравнение:
, имеет общее уравнение:
А) 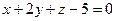 ; Б)
; Б) 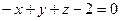 ; В)
; В) 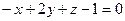 ; Г)
; Г) 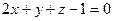 .
.
6.20. Плоскости 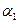 и
и 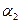 заданы уравнениями:
заданы уравнениями: 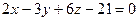 ,
, 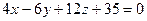 . Расстояние между плоскостями
. Расстояние между плоскостями 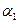 и
и 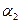 равно:
равно:
А) 2,5; Б) 3,5; В) 4,5; Г)5,5.
6.21. Плоскости 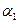 и
и 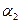 заданы уравнениями:
заданы уравнениями: 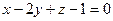 ,
, 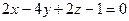 . Расстояние между плоскостями
. Расстояние между плоскостями 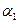 и
и 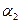 равно:
равно:
А) 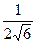 ; Б)
; Б) 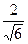 ; В)
; В) 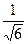 ; Г)
; Г) 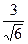 .
.
6.22. Канонические уравнения прямой 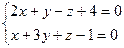 имеют вид:
имеют вид:
А) 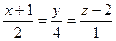 ; Б)
; Б) 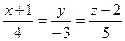 ; В)
; В) 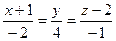 ; Г)
; Г) 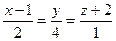 .
.
6.23. Если плоскость 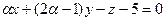 перпендикулярна к плоскости
перпендикулярна к плоскости 
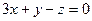 , то значение ά равно:
, то значение ά равно:
А) 0; Б)1; В)2; Г)3.
6.24. Если прямые 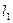 и
и 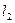 заданы уравнениями:
заданы уравнениями: 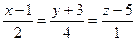 ,
, 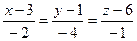 , то:
, то:
А) 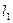 и
и 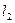 параллельны; Б)
параллельны; Б) 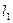 и
и 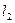 пересекаются; В)
пересекаются; В) 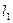 и
и 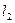 скрещиваются; Г)
скрещиваются; Г) 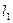 и
и 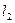 совпадают
совпадают
6.25. Плоскость α, проходящая через начало координат и точки А (3;-2;1) и В (1;4;0), имеет общее уравнение:
А) 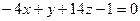 ; Б)
; Б) 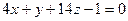 ; В)
; В) 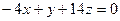 ; Г)
; Г) 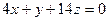 .
.
6.26. Канонические уравнения прямой 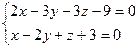 имеют вид:
имеют вид:
А) 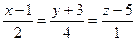 ; Б)
; Б) 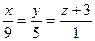 ; В)
; В) 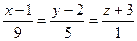 ; Г)
; Г) 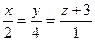 .
.
6.27. Проекция точки А (4;-3;1) на плоскость 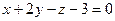 имеет координаты:
имеет координаты:
А) (1;0;-2); Б) (2;1;1); В) (3;1;2); Г)(5;-1;0).
6.28. Если плоскость 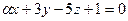 параллельна прямой
параллельна прямой 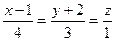 , то значение ά равно:
, то значение ά равно:
А) -2; Б) 0; В) -1; Г) 1.
6.29.Даны две точки А (1;3;-2) и В (7;-4;4). Плоскость α, проходящая через точку В перпендикулярно к прямой АВ, имеет общее уравнение:
А) 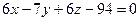 ; Б)
; Б) 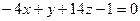 ; В)
; В) 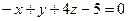 ; Г)
; Г) 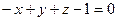 .
.
6.30. Плоскость α, проходящая через точки А (0;6;4), В (3;5;3) и С (1;-1;4), имеет общее уравнение:
А) 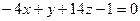 ; Б)
; Б) 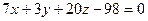 ; В)
; В) 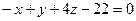 ; Г)
; Г) 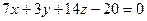 .
.
6.31. Точка М, симметричная началу координат относительно плоскости 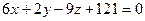 , имеет координаты:
, имеет координаты:
А) (12;-4;18); Б) (-12;-4;18); В) (-12;-4; 8); Г) (-2;-4;18).
6.32. Угол между плоскостями 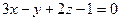 и
и 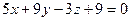 равен:
равен:
А) 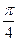 ; Б)
; Б) 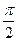 ; В)
; В) 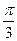 ; Г)
; Г) 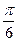 .
.
6.33. Если плоскость 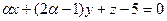 параллельна плоскости
параллельна плоскости 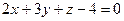 , то значение ά равно:
, то значение ά равно:
А)1; Б) -1; В) -2; Г) 2.
6.34 Плоскость, проходящая через две параллельные прямые 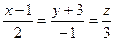 и
и 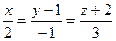 , имеет уравнение:
, имеет уравнение:
А) 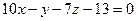 ; Б)
; Б) 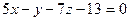 ;
;
В) 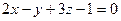 ; Г)
; Г) 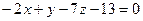 .
.
6.35 Угол между прямой 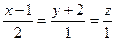 и плоскостью
и плоскостью 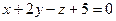 равен:
равен:
А) 45°; Б) 90°; В) 30°; Г) 60°.
6.36. Прямая 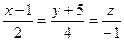 параллельна плоскости
параллельна плоскости 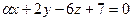 , если значение α равно:
, если значение α равно:
А) -6; Б) -5; В) 0; Г) -7.
6.37 Угол между прямой 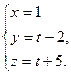 и плоскостью
и плоскостью 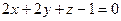 равен:
равен:
А) 60°; Б) 45°; В) 30°; Г) 90°.
6.38.Если прямая 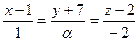 параллельна плоскости
параллельна плоскости 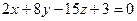 , то значение α:
, то значение α:
А) -2; Б) 0; В) -4; Г) 1.
6.39. Плоскость α, проходящая через ось Ох и параллельная вектору 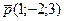 , имеет общее уравнение:
, имеет общее уравнение:
А) 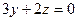 ; Б)
; Б) 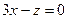 ; В)
; В) 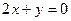 ; Г)
; Г) 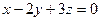 .
.
6.40. Плоскость α, проходящая через ось Оу и параллельная вектору 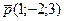 , имеет общее уравнение:
, имеет общее уравнение:
А) 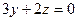 ; Б)
; Б) 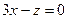 ; В)
; В) 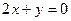 ; Г)
; Г) 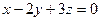 .
.
6.41. Плоскость α, проходящая через ось Оz и параллельная вектору 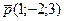 , имеет общее уравнение:
, имеет общее уравнение:
А) 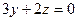 ; Б)
; Б) 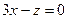 ; В)
; В) 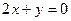 ; Г)
; Г) 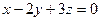 .
.
6.42. Плоскость α, проходящая через точку 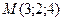 и отсекающая на осях координат одинаковые отрезки
и отсекающая на осях координат одинаковые отрезки 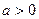 , имеет общее уравнение:
, имеет общее уравнение:
А) 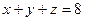 ; Б)
; Б) 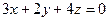 ; В)
; В) 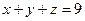 ; Г)
; Г) 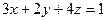 .
.
6.43. Если точка 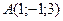 служит основанием перпендикуляра, проведенного из начала координат на плоскость α, то плоскость α имеет общее уравнение:
служит основанием перпендикуляра, проведенного из начала координат на плоскость α, то плоскость α имеет общее уравнение:
А) 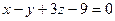 ; Б)
; Б) 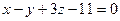 ; В)
; В) 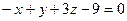 ; Г)
; Г) 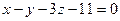 .
.
6.44. Плоскость α проходящая через ось Оz и параллельная прямой 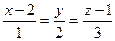 , имеет общее уравнение:
, имеет общее уравнение:
А) 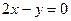 ; Б)
; Б) 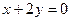 ; В)
; В) 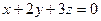 ; Г)
; Г) 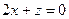 .
.
6.45. Укажите, какие из точек М 1(3;4;7), М 2(2;0;4), М 3(-1;3;2) принадлежат прямой 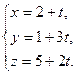
А) М 1 и М 2; Б) М 1; В) М 2; Г) М 3.
6.46. Если плоскости 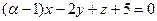 и
и 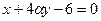 перпендикулярны, то значение α равно:
перпендикулярны, то значение α равно:
А) 7; Б)-7; В) 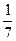 ; Г)
; Г) 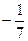 .
.
6.47 Проекция точки 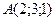 на прямую
на прямую 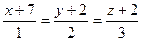 имеет координаты:
имеет координаты:
А) 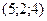 ; Б)
; Б) 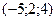 ; В)
; В) 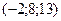 ; Г)
; Г) 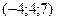 .
.
6.48 Если прямая 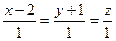 принадлежит плоскости
принадлежит плоскости 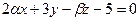 , то значения α и β равны:
, то значения α и β равны:
А) α = 2, β = 7; Б) α = -2, β = 3; В) α = 0, β = 3; Г) α = 1, β = 5.
6.49 Если прямая 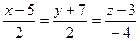 перпендикулярна к плоскости
перпендикулярна к плоскости 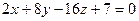 , то значение α равно:
, то значение α равно:
А) 2; Б) 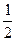 ; В)-80; Г) -2.
; В)-80; Г) -2.
6.50 Косинус угла между прямой 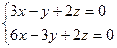 и осью Оу равен:
и осью Оу равен:
А) 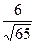 ; Б)
; Б) 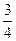 ; В)
; В) 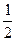 ; Г)
; Г) 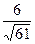 .
.
 2015-04-12
2015-04-12 393
393






