Расстояние между двумя точками 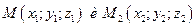 пространства находятся по формуле:
пространства находятся по формуле: 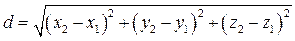
Координаты 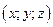 точки М—середины отрезка с концами
точки М—середины отрезка с концами 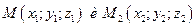 находятся по формуле:
находятся по формуле: 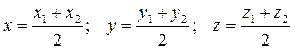 .
.
Уравнение прямой:
· С угловым коэффициентом 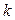 и начальной ординатой
и начальной ординатой 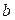 :
: 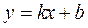 ;
;
· Проходящей в данном направлении (с угловым коэффициентом 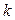 ) через данную точку
) через данную точку 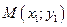
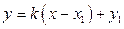 ;
;
· Проходящей через две данные точки 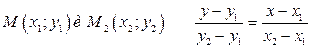
· Общее уравнение прямой 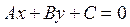 , где
, где 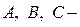 постоянные коэффициенты, причем А и В одновременно не обращаются в нуль
постоянные коэффициенты, причем А и В одновременно не обращаются в нуль 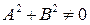 .
.
· Уравнение прямой в отрезках: 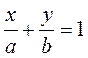 , где
, где 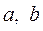 --длины отрезков (с учетом знаков), отсекаемой прямой на осях
--длины отрезков (с учетом знаков), отсекаемой прямой на осях 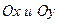 соответственно.
соответственно.
· Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле: 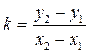 , где
, где 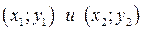 --координаты данных точек.
--координаты данных точек.
Если две прямые лежат в одной плоскости:
· Под углом между прямыми в плоскости понимают наименьший (острый) из двух смежных углов, образованными этими прямыми: 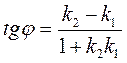 , где
, где 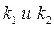 --угловые коэффициенты данных прямых.
--угловые коэффициенты данных прямых.
· Условие параллельности прямых 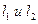 имеет вид:
имеет вид: 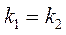 , а условие их перпендикулярности:
, а условие их перпендикулярности: 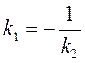
· Если прямые 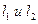 заданы общими уравнениями
заданы общими уравнениями 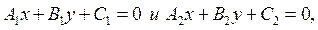 то величина
то величина 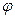 угла между ними
угла между ними
определяется по формуле: 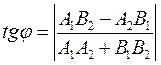 ,
,
условие их параллельности: 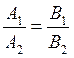 ,
,
а условие их перпендикулярности: 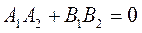 .
.
· Расстоянием 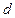 от точки
от точки 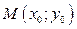 до прямой
до прямой 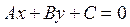 называется длина перпендикуляра, опущенного из этой точки на прямую:
называется длина перпендикуляра, опущенного из этой точки на прямую: 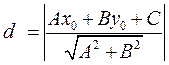 .
.
 2015-04-12
2015-04-12 252
252








