Пример 1. Действия с матрицами
Вычислим матрицу 2A-BA, где 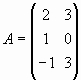 и
и 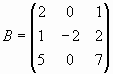 .
.
Вычислим матрицу 2A - BA.
Определим матрицу A размерности 3 x 2:
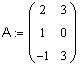
Чтобы определить матрицу, введите с клавиатуры имя матрицы и знак присваивания (его можно ввести щелчком по соответствующей позиции в панели EvaluationToolbar панели математических инструментов). Затем щелкните по кнопке MatrixorVectorToolbar в панели математических инструментов, чтобы открыть панель операций с матрицами и векторами. Откройте щелчком по кнопке MatrixorVector окно диалога InsertMatrix, определите число строк (Rows) и число столбцов (Columns) и закройте окно диалога, щелкнув по кнопке Ok.
Определим матрицу B размерности 3 x 3:
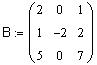
Вычислим матрицу C=2A размерности 3 x 2:
Знак присваивания можно ввести щелчком по соответствующей позиции в панели Evaluation.
Знак умножения можно ввести, используя клавишу <*>.
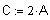
Для просмотра результата умножения введите после имени матрицы C знак равенства, используя клавишу <=>.
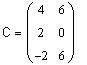
Вычислим матрицу D=BA размерности 3 x 2:
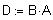
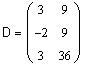
Вычислим матрицу 2A-BA размерности 3 x 2, равную матрице C-D:
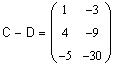
Пример 2. Проверка перестановочности матриц
Проверим, что матрицы 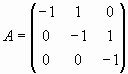 и
и 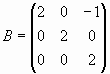 перестановочны, а матрицы А и
перестановочны, а матрицы А и 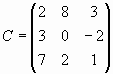 неперестановочны.
неперестановочны.
Проверка перестановочности матриц A и B, A и C
Определим матрицы A, B и C:
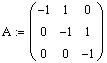
Чтобы определить матрицу, введите с клавиатуры имя матрицы и знак присваивания (его можно ввести щелчком по соответствующей позиции в панели EvaluationToolbar панели математических инструментов). Затем щелкните по кнопке MatrixorVectorToolbar в панели математических инструментов, чтобы открыть панель операций с матрицами и векторами. Откройте щелчком по кнопке MatrixorVector окно диалога InsertMatrix, определите число строк (Rows) и число столбцов (Columns) и закройте окно диалога, щелкнув по кнопке Ok.
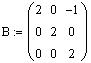
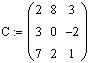
Найдем произведения матриц AB и BA
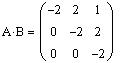
Знак умножения можно ввести, используя
клавишу <*>.
Для просмотра результата умножения введите знак равенства, используя клавишу <=>.
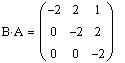
Матрицы A и B перестановочны, т.к. AB=BA.
Найдем произведения матриц AC и CA
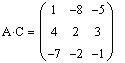
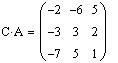
Матрицы A и C неперестановочны, т.к. 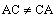
Пример 3. Умножение матрицы на матрицы специального вида
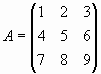
Умножим матрицу на единичную, скалярную и матрицы
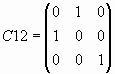 и
и 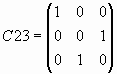 .
.
Умножим матрицу A на единичную, скалярную матрицы и матрицы С12, С23.
Определим матрицу A:
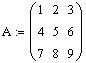
Чтобы определить матрицу, введите с клавиатуры имя матрицы и знак присваивания (его можно ввести щелчком по соответствующей позиции в панели EvaluationToolbar панели математических инструментов). Затем щелкните по кнопке MatrixorVectorToolbar в панели математических инструментов, чтобы открыть панель операций с матрицами и векторами. Откройте щелчком по кнопке MatrixorVector окно диалога InsertMatrix, определите число строк (Rows) и число столбцов (Columns) и закройте окно диалога, щелкнув по кнопке Ok.
Сформируем единичную матрицу E и скалярную матрицу E2 порядка 3 с помощью встроенной функции identity(n) Mathcad:

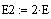
Знак присваивания можно ввести щелчком по соответствующей позиции в панели Evaluation.
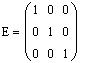
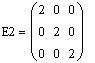
Для просмотра результата введите знак равенства после имени матрицы, используя клавишу <=>.
Умножение матрицы A на единичную матрицу
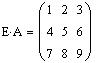
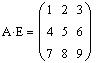
Знак умножения можно ввести, используяклавишу <*>.
Умножение матрицы A на число, умножение на скалярную матрицу E2:
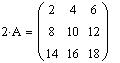
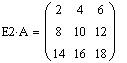
Таким образом, умножением матрицы на скалярную матрицу можно реализовать операцию умножения матрицы на число.
Перестановка строк и столбцов матрицы осуществляется умножением на матрицы специального вида. Покажем это на примере матрицы A.
Определим матрицы C12 и C23:
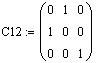
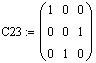
Перестановка двух строк матрицы A:
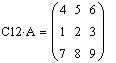
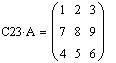
Перестановка двух столбцов матрицы A:
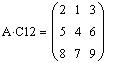
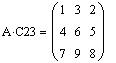
Пример 4. Возведение матрицы в степень
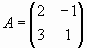
Для матрицы найдем A0, A1, A2.
Для матрицы A найдем матрицы 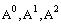 .
.
Определим матрицу A:
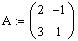
Чтобы определить матрицу, введите с клавиатуры имя матрицы и знак присваивания (его можно ввести щелчком по соответствующей позиции в панели EvaluationToolbar панели математических инструментов). Затем щелкните по кнопке MatrixorVectorToolbar в панели математических инструментов, чтобы открыть панель операций с матрицами и векторами. Откройте щелчком по кнопке MatrixorVector окно диалога InsertMatrix, определите число строк (Rows) и число столбцов (Columns) и закройте окно диалога, щелкнув по кнопке Ok.
Возведем матрицу A в степень 0, 1, 2:

Для возведения матрицы в степень по соответствующей позиции панели CalculatorToolbar панели математических инструментов.
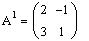
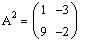
Для просмотра результата введите знак равенства, используя клавишу <=>.
Пример 5. Обращение матрицы
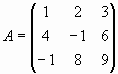
Проверим, что матрица невырождена и найдем матрицу A-1.
Проверим, что матрица A невырождена и найдем обратную матрицу
Определим матрицу A:
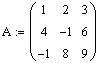
Чтобы определить матрицу, введите с клавиатуры имя матрицы и знак присваивания (его можно ввести щелчком по соответствующей позиции в панели EvaluationToolbar панели математических инструментов). Затем щелкните по кнопке MatrixorVectorToolbar в панели математических инструментов, чтобы открыть панель операций с матрицами и векторами. Откройте щелчком по кнопке MatrixorVector окно диалога InsertMatrix, определите число строк (Rows) и число столбцов (Columns) и закройте окно диалога, щелкнув по кнопке Ok.
Найдем определитель матрицы A:
Для нахождения определителя матрицы, воспользуйтесь нопкойDeterminant в панели MatrixorVectorToolbar.
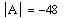
Для просмотра результата введите знак равенства, используя клавишу <=>.
М атрица A невырождена, т.к. ее определитель не равен 0; следовательно, обратная матрица 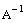 существует.
существует.
Найдем матрицу 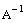 :
:

Для нахождения обратной матрицы, воспользуйтесь кнопкой Inverse в панели MatrixorVectorToolbar.
Найдем 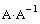 и
и 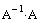 :
:
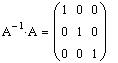
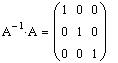
Знак умножения можно ввести, используя клавишу <*>
Пример 6. Ортогональная матрица
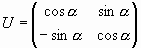
Проверим, что матрица ортогональна.
Проверим, что матрица U ортогональна (используя символьные вычисления Mathcad)
Определим матрицу U:
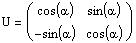
Для определения символьной матрицы введите с клавиатуры ее имя, символьный знак равенства < = > (его можно ввести щелчком по соответствующей позиции в панели BooleanToolbar). Затем щелкните по кнопке MatrixorVectorToolbar в панели математических инструментов, чтобы открыть панель операций с матрицами и векторами. Откройте щелчком по кнопке MatrixorVector окно диалога InsertMatrix, определите число строк (Rows) и число столбцов (Columns) и закройте окно диалога, щелкнув по кнопке Ok. После этого введите элементы матрицы.
Символ a можно ввести щелчком по соответствующей позиции в панели Greek SymbolToolbar.
Убедимся, что матрица U невырождена:
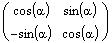
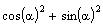
Символьные операция вычисления определителя выполняется через меню символьных операций Symbolics. Заключите символьную матрицу в выделяющую рамку (щелкните по любому элементу и нажимайте клавишу <Space> пока выделяющая рамка не охватит всю матрицу), затем выберите операцию Determinant в пункте Matrix меню Symbolics.
Чтобы упростить выражение для определителя матрицы U, заключите выражение в выделяющую рамку и выберите пункт Symplify в меню Symbolics.
Найдем обратную матрицу 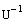 и транспонированную матрицу
и транспонированную матрицу 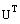
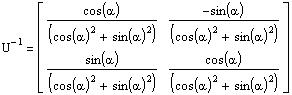
Символьные операции транспонирования и обращение выполняются через меню символьных операций Symbolics. Заключите символьную матрицу в выделяющую рамку (щелкните по любому элементу и нажимайте клавишу <Space> пока выделяющая рамка не охватит всю матрицу), затем выберите нужную операцию в пункте Matrix меню Symbolics.
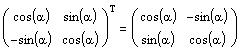
Для ввода 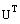 нужно щелкнуть по соответствующей кнопке панели VectororMatrixToolbar.
нужно щелкнуть по соответствующей кнопке панели VectororMatrixToolbar.
Так как 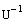 =
= 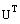 , матрица U ортогональна.
, матрица U ортогональна.
 2015-04-12
2015-04-12 475
475







