Перпендикулярная поляризация

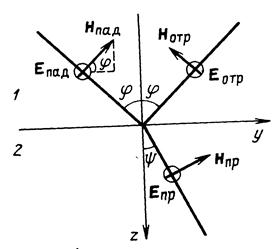
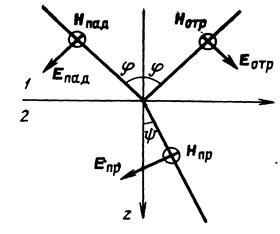
Рис. 2. Перпендикулярная поляризация падающей волны

Формулы для расчета коэффициентов отражения и преломления при перпендикулярной поляризации (рис. 2) имеют следующий вид:

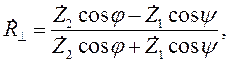	(2.3)
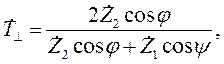	(2.4)

где R_┴ - коэффициент отражения, T_┴ - коэффициент прохождения, Z₁ - волновое сопротивление среды, из которой падает волна, Z₂ - волновое сопротивление среды, на границу с которой падает волна.

Так как в общем случае все волновые сопротивления, входящие в формулы (2.3) и (2.4) – величины комплексные, коэффициенты отражения и преломления целесообразно представить в следующем виде:

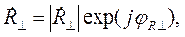	(2.5)
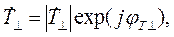	(2.6)

где:

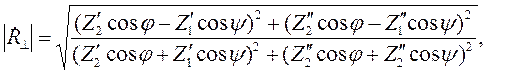	(2.7)
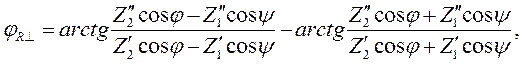	(2.8)
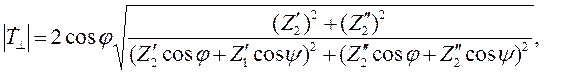	(2.9)
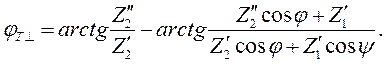	(2.10)

В формулах (2.7) – (2.10) одним штрихом помечена действительная часть комплексного волнового сопротивления, а двумя штрихами – мнимая часть.

Этих формул достаточно для того, чтобы рассчитать модули и фазы коэффициентов отражения и преломления при перпендикулярной поляризации. Однако чаще всего в качестве среды 1 выступает диэлектрик без потерь с относительными проницаемостями ε₁ и μ₁. В этом случае формулы (2.7) – (2.10) примут вид:

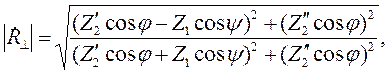	(2.11)
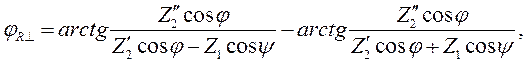	(2.12)
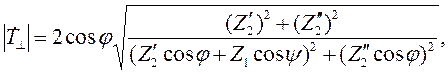	(2.13)
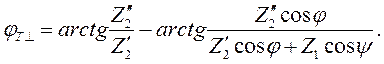	(2.14)

Формулы (2.5) - (2.14) пригодны и для расчета коэффициентов отражения и прохождения при падении волны по нормали к поверхности раздела. Очевидно, что в этом случае поляризация также является перпендикулярной. Для расчета коэффициентов в формулах надо положить φ = ψ = 0. При этом все косинусы углов станут равными единице и формулы существенно упростятся.

Рис. 3. Параллельная поляризация падающей волны